Доказано[1], что в любом достаточно большом множестве точек в общем положении содержится выпуклый пустой шестиугольник. Но существуют сколь угодно большие множества точек в общем положении, в которых нет выпуклого пустого семиугольника[2]. Вопрос о необходимом числе точек по сей день остаётся открытым. Известно, что требуется не менее 30 точек[3]. А если справедлива гипотеза Эрдёша-Секереша о многоугольниках, то не более 129[4].
Правильный шестиугольникПравильный шестиугольник
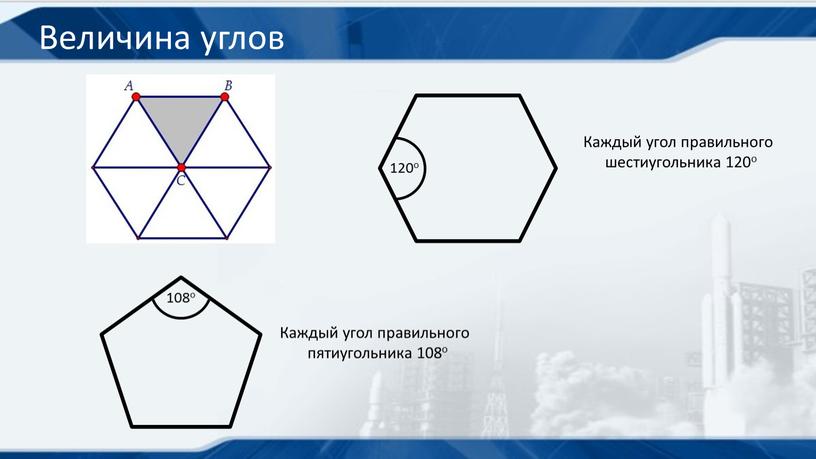
Правильным называется шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Звездчатые шестиугольники
Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника, называется звёздчатым. Помимо правильного существует ещё один звёздчатый шестиугольник, состоящий из двух правильных треугольников — гексаграмма или звезда Давида.
См.
также
такжеПримечания
- ↑ Nicolás, Carlos M. (2007), «The empty hexagon theorem»,
- ↑ Horton, J. D. (1983), «Sets with no empty convex 7-gons», Canadian Mathematical Bulletin Т. 26 (4): 482–484, DOI 10.4153/CMB-1983-077-8
- ↑ Overmars, M. (2003), «Finding sets of points without empty convex 6-gons», Discrete and Computational Geometry Т. 29 (1): 153–158, DOI 10.1007/s00454-002-2829-x
- ↑ Gerken, Tobias (2008), «Empty convex hexagons in planar point sets», Discrete and Computational Geometry Т. 39 (1–3): 239–272, DOI 10.1007/s00454-007-9018-x
8.1. Шестиугольник. Разоблаченный логотип, или Психогеометрия
8.1. Шестиугольник
Да что там хваленый немецкий порядок. Вот у муравьев – настоящий «орднунг». И чего они не стали хозяевами планеты?
Козьма Прутков, сельский учитель, бывший фронтовик
Шестиугольная плитка крепче держится.
Мнение штукатуров
Вместе весело шагать по просторам, по просторам!
Из детской песенки
Разом нас багато, нас не подолати.
Непереводимый слоган 2004 года
Медовые соты вкуснейшая вещь, да уж слишком больно обходятся.
Медведь Мишка
Дресс-код – та же униформа, только в мирное время.
Из корпоративного этикета
Мы едины или просто все клонированы?
Открытый вопрос
ШЕСТИУГОЛЬНИК – особая фигура, аналогов у которой поистине нет. Она обладает свойством, которое нигде больше не повторяется так ярко, функционально и выразительно. А для нашей цивилизации еще и предельно актуально. На современном языке это именуется «корпоративным духом» и «корпоративной религией». Впрочем, можно додуматься и до «бренд-рая» на основе все той же корпоративной религии[3].
Но давайте вначале рассмотрим психогеометрическую сущность самого шестиугольника. Его изображение представлено на рис. 8.1. У фигуры отчетливо выражен центр.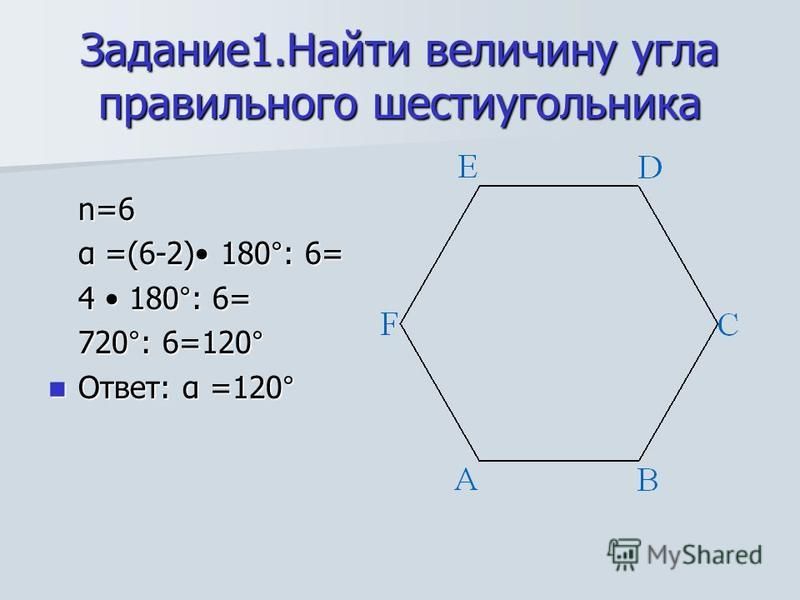
В этом аспекте шестиугольник чем-то сродни кругу. Однозначно есть своя идеология, единство и целостность. Шестиугольник обладает ярко выраженной самостью. Поэтому во внешних «варягах» совершенно не нуждается. Управление из центра идет по стратегическим радиальным каналам по направлению к углам. Административная иерархия четко прослеживается. Проще говоря, шестиугольник знает, что нужно делать, и умеет эффективно выстроить свой менеджмент.
Есть два ударных угла. Что весьма немаловажно. Можно концентрировать силы на главных направлениях. А в общем-то, в наличии еще четыре дополнительных угла по круговой обороне, потому-то и шестиугольник. Попробуй подкатись без тщательной рекогносцировки. Шестиугольник умеет очень хорошо защищать свою территорию и свои интересы вовне ее. Своего рода скрытая агрессия, неумолимая и весьма беспощадная. Железно работает правило: «кто не с нами – тот против нас». Однако авантюрного риска в этой фигуре совершенно нет. Исключено.
Обратим также внимание на внутренние производственные возможности, на рисунке зона производства заштрихована (рис.
8.2). Шестиугольник особенно удачно сочетает логику и иррациональность в своей тактике и стратегии. Где надо – работать, где надо – атаковать (углы-то выступающие). Добавьте к этому единство идеологии и диктат центра. Поистине неотразимое сочетание. И все как-то целостно объединено.
Но главная фишка все же в другом. Шестиугольник может. производить себе подобных! Скажем, для круга, треугольника либо овала это просто физически невозможно, да и немыслимо. Зато шестиугольник очень легко объединяется с себе подобными в некую ячеистую сеть, которая непрерывно множится (рис. 8.3). Такова уж его конфигурация. Она позволяет устанавливать связи в самых различных направлениях. Создавая, например, сеть однотипных филиалов. Что и есть отличительным признаком корпорации (от позднелатинского corporatio – объединение, сообщество). Впрочем, можно применять термин «множение» либо «клонирование». Наверное, это так увлекательно – бесконечно расширяться и строить мир по своему плану и подобию. Идея, многократно воспроизведенная, становится очевидным материальным и духовным могуществом.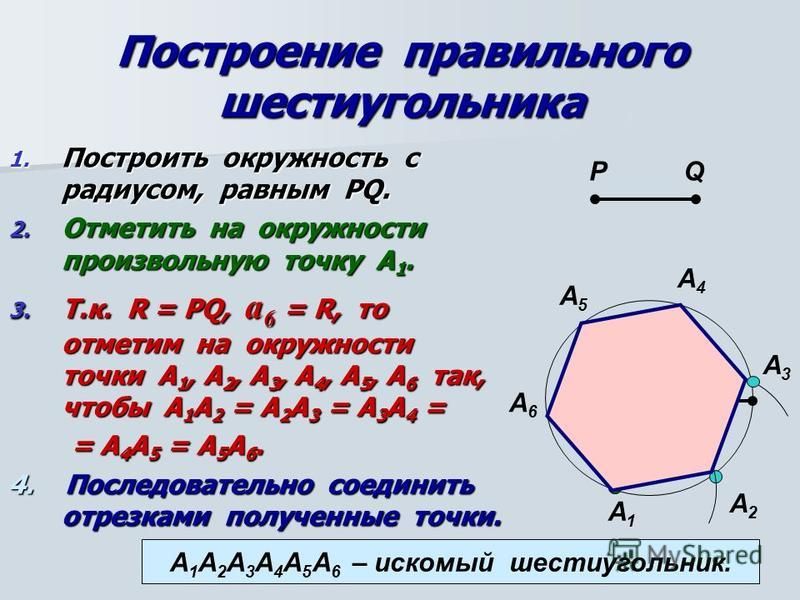
Да, еще несколько слов о пространственном положении фигуры. Шестиугольник весьма самодостаточен, автономен, идеологичен, он обладает собственной базой воспроизводства, и потому ему, как и ромбу, больше всего подходит вертикальное положение, когда ударные углы смотрят вверх и вниз (рис. 8.1). Но бывают ситуации, когда шестиугольник вынужден ложиться на бок (рис. 8.5). Скорее всего, из-за чисто прагматических интересов.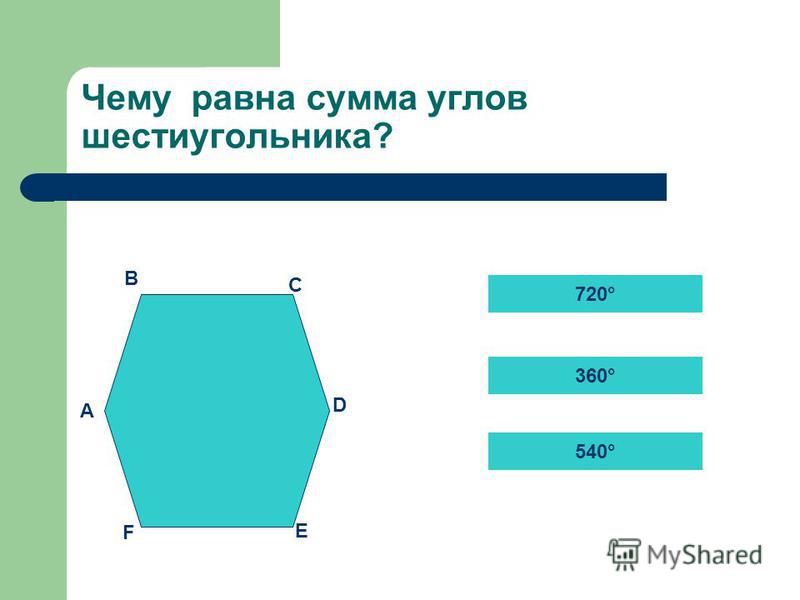
ЛЮДИ И ФИРМЫ КОРПОРАТИВНОГО ДУХА. Здесь ответ однозначен – им это очень нравится. Достигать высот можно различными путями. В данном случае лучше под надежной и могущественной крышей.
Сопричастность к великому делу порой захватывает дух не хуже любого индивидуального экстрима. И при этом есть масса плюсов. Прежде всего не надо терзаться со смыслом жизни, личной миссией, вечными «гамлетовскими» вопросами и прочими неврозами выбора и принятия решения. Корпоративная религия в прямом смысле даст покой душе. Что в наше время очень даже немало. Стимул к успеху также налицо. Финансовое поощрение, атрибуты власти, чувство собственной значимости мало кого оставят равнодушными. Остается лишь денно и нощно стараться не выпасть из генерального русла. Люди корпоративного духа всегда исполнительные и превосходные работники. Им нравится по утрам облачаться в «деловую униформу» и с наслаждением приступать к порученным делам. Соты множатся, и это приятно. Причитающееся вознаграждение – тем более. И после затяжных праздничных выходных опять тянет обрести привычный смысл «времяпрожития» в офисе, с которым уже почти сроднился. Тем более что преданность и деловой энтузиазм (а если он еще и сверхактивный) корпорацией только поощряются.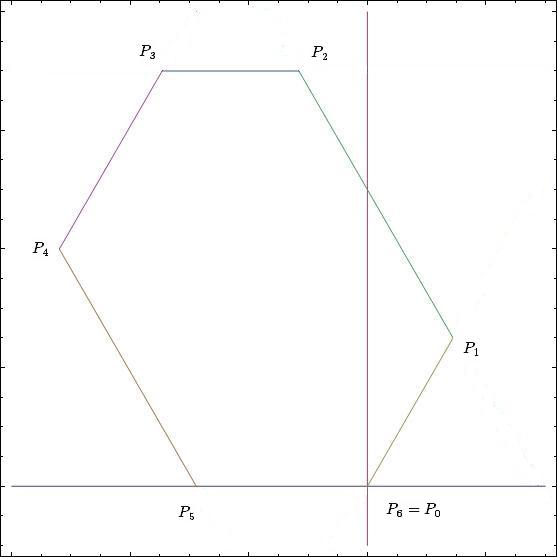
Никаких сомнений и только сплошной позитив в работе, общении и, безусловно, настроении. Пожалуй, по психологической атмосфере коммунистические субботники эпохи начала строительства советского социализма здесь могут и проигрывать. Для корпоративного духа важна исключительно добровольная мотивация быть сопричастным. Снова подчеркнем – не безвозмездно. Особенно для адептов (фр. adepte – сторонник, приверженец, лат. adeptus – достигший) от бизнеса.
Для фирмы, правда, очень бурный корпоративный рост может сыграть плохую шутку. Все оборотные и наличные активы окажутся втянутыми в дело. Свободные деньги иссякнут, и может возникнуть угроза локального дефолта по неотложным платежам. А если еще незаметно подкрадется более глобальный кризис мирового сообщества, тогда станет совсем плохо. Корпорации, в отличие от фирм, гораздо легче идут с молотка по столь низкой цене, о которой даже никогда и не мечталось. Работники будут несказанно шокированы. Как же так? Незыблемый дотоле муравейник вдруг разорен! Подобный суперстресс корпоративному человеку весьма трудно будет пережить.
Придется стремглав подыскивать новую ячейку. А в общем-то, корпорации и их работники очень боятся любых перемен. И уж тем более непредсказуемых, а то и угрожающих вызовов внешней среды и эпохи. Как, впрочем, и любая другая империя. Но здесь стабильность и величие именно в создании сети по единому образу и подобию, исходя из первоначального эскиза. Шестиугольники (человек и фирма) терпеливы и могут долго ждать своего часа для успешного клонирования. Сотовая сеть сразу и просто так не возникает. Ей предшествует скрытый от посторонних глаз латентный период. Поэтому до конца всю правду вы так и не узнаете. Публичность и откровенность все же разные вещи.
СОТОВЫЙ КОНТАКТ, или ДЕЛОВАЯ КОММУНИКАЦИЯ ШЕСТИУГОЛЬНИКА. Уже сама постановка вопроса слегка проблематична. Шестиугольнику, который сам себя воспроизводит, союзники и партнеры не особенно-то и нужны. По идее. На практике все несколько иначе. Сотовое клонирование имеет как своих союзников, так и врагов. Нейтралитет, впрочем, тоже возможен, но лишь до поры до времени.
Экспансия – она и есть экспансия, даже если существует лишь в одиночном проекте.
С квадратом и прямоугольником может наблюдаться нечто вроде симбиоза. Все-таки нужда в производственном аспекте требует системности, рационального подхода и отлаженного хода воспроизводства. Главное, чтобы квадрат ни в коем случае не мешал корпоративному расширению. Сравните рис. 8.6 и 8.7. В первом случае с гармонией несколько не сложилось. Квадрат не позволяет ему вовсю клонироваться. Да и сама рациональная система квадрата серьезно подменена чужеродным корпоративным духом. Рано или поздно шестиугольник сбросит оболочку квадрата, использовав ее лишь как мимикрию. На рис. 8.7 ситуация гораздо благоприятнее. Вместо иррациональной корпоративной харизмы шестиугольника – исключительно голый расчет и строго системный подход во всех делах. Штаб-квартира в виде квадрата диктует свою волю будущему клонированию и созданию сети.
Вариант наиболее удачного симбиоза с прямоугольником уже показан на рис. 8.
2. Только полное слияние и тотальное растворение прямоугольника в структуре шестиугольника. Другие варианты не рассматриваются.
С кругом у шестиугольника общая склонность к идеологическому центру. Ну а два идеолога, да еще «центровых», далеко не всегда находят общий язык. Тем более что круг иррационален и мистичен, а шестиугольник скорее рационалист и руководствуется сугубо прагматичным подходом в своих делах. Поэтому представить шестиугольник внутри круга можно (рис. 8.8), но, как и в случае с наружным квадратом, гармонии здесь нет. Круг уж больно не любит что-либо впускать внутрь себя, да еще в зоне сакральной идеи. Все, ей теперь конец. Там уже диктат идеологии шестиугольника. Хотя и шестиугольнику не совсем уютно. Из круга как-то надо будет вырваться. А круги не склонны просто за так кого-либо из своих объятий выпускать. А вдруг удастся переделать шестиугольник под себя? Все-таки некое тождество наличествует.
Но вот если круг окажется внутри шестиугольника (рис. 8.9), то можно смело предположить, что внутри корпорации имеется еще один, более закрытый идеологический центр.
Корпоративный дух служит некой наружной оболочкой, что, однако, не мешает корпорации развиваться. До тех пор пока круг не начнет ради своих идей отбирать слишком много оборотных средств. А так, скорее всего, и будет. Если босс со своим ближайшим окружением вдруг увлекся религией, то менеджеры-практики начнут подыскивать другое рабочее место. Тандем «корпорация + религия» – это все же не «корпоративная религия». Но тем не менее в наше время подобное слияние только набирает обороты.
Но вот с треугольником и ромбом никакого глубокого идейного слияния у шестиугольника не предвидится. Для объяснения почему, здесь даже рисунков не требуется. Эти фигуры по своей жесткой и независимой природе не склонны куда-либо инкорпорироваться. Корпорация их может использовать только методом аутсорсинга, т. е. временные контракты для оказания определенной услуги. Шестиугольник, тем более в сотовом варианте, не любит идти на слишком большой риск. Есть, что терять. Треугольнику и ромбу это как раз не страшно, ибо они для такой работы и предназначены.
Но вот с корпоративным духом будет посложней. Строптивость, видите ли. Да и нежелание годами высиживать карьеру.
С овалом, овоидом и каплей тоже судьба не сложится. Уж больно разный стиль жизни и решаемые задачи. Миссия тоже совершенно разная. Тем более что названные фигуры динамичны, а шестиугольник таковым не является. Опять же, тот же овоид имеет свою идеологию и знает, куда двигаться. Биполярный овал внесет только ненужную полярность для центричного шестиугольника. А у капли слишком короткий срок жизни. Стабильной корпорации такой сценарий и даром не нужен. Сеть должна в своем существовании стремиться к вечности.
МОНОЦВЕТИЕ КОРПОРАТИВНОЙ СТРУКТУРЫ. Пожалуй, начнем с того, что для логотипов шестиугольник очень даже подходит. Особенно если будет красиво выложен фрагмент ячеистой структуры (см. рис. 8.3). Все хотят быть стабильными и развивающимися. Да еще и согласно своему стратегическому бизнес-плану. Осталось лишь удачно выбрать корпоративный стиль. И цветовое решение логотипа, в котором шестиугольник – ключевая фигура.
Белый шестиугольник динамично стремится в будущее, легко находит альтернативы своего клонирования, привлекает партнеров и работников. Но у него «забелены» истоки и, собственно, сама корпоративная миссия. Такое ощущение, что корпорация непрерывно находится в поиске чего-то нового. Может быть, в этом и суть миссии? В любом случае сочетание цвета и формы здесь неожиданно, но может сработать.
Желтый, равно как и оранжевый, добавит позитивной активности, но внесет легкомыслие и повышенную трату ресурсов. Для корпорации не совсем подходящий вариант. Разве что она специализируется на дорожно-строительных работах. Там действительно много тратят и почти всегда не укладываются в смету.
Зато отлично подойдет глубокий золотистый цвет. Лучше без полировки, т. е. не зеркальный. Престижность и уверенность. И никаких сомнений. Успех корпорации будет всегда обеспечен!
Алый шестиугольник активный и весьма импульсивно атакующий среду. Корпоративный дух едва ли не приравнен к духу боевому.
Чем-то напоминает самурайство в бизнесе. Можно и так развивать сеть. Хотя темновато-красный шестиугольник уже более глубокий и уравновешенный, при сохранении корпоративной «боевитости». Но еще лучше – вишневый и пурпурный. Поистине императорские цвета, а корпорации именно это и нужно. Глубина развертывания сотовой сети только усилится за счет чувствования внутренних и внешних процессов без ослабления мощи экспансии. Только теперь она будет более взвешенной. Малиновый еще больше усилит коммуникативные качества корпоративного духа как внутри структуры, так и с внешней средой, но слабым малиновый шестиугольник казаться не будет.
Соты черного цвета покажутся уж очень мрачными и, следовательно, потерявшими вкус к жизни. Черный сжимает и уходит вглубь, а здесь как раз и нужны активная внешняя экспансия и позитивный имидж развертывания сети. Не подойдет черный цвет для корпоративных задач.
Серый в любых оттенках, кроме очень бледного, а также серебристо-серый очень даже ничего.
Хорошая динамика, отлично разработанные стратегия и тактика продвижения, внимания к внешней среде и мощная аналитика собственных проблем и задач. Полная толерантность и внимание ко всему. В сером цвете корпорацию точно лихорадить не будет. Все будет происходить без эксцессов, что для шестиугольника немаловажно.
Цвет металла шестиугольникам надо также избегать. Внешняя среда начнет более активно сопротивляться политике экспансии. И тогда сотовая сеть начнет восприниматься агрессивно. Зачем это делать?
Намного лучше темно-синий, а также фиолетовый цвет. У структуры появляется внутренняя глубина процессов и собственно самого корпоративного духа. Чувство внешней среды также усилится. Главное, чтобы корпоративный дух постепенно не подменился духом религиозным. Тогда уже будет не до дальнейшего развертывания. Зато комфортно в слитном единстве.
Хотите, чтобы в коллективах корпорации сохранялись дружелюбные отношения между коллегами и работа не воспринималась как трудовая повинность? Тогда выбирайте приятный голубой, т.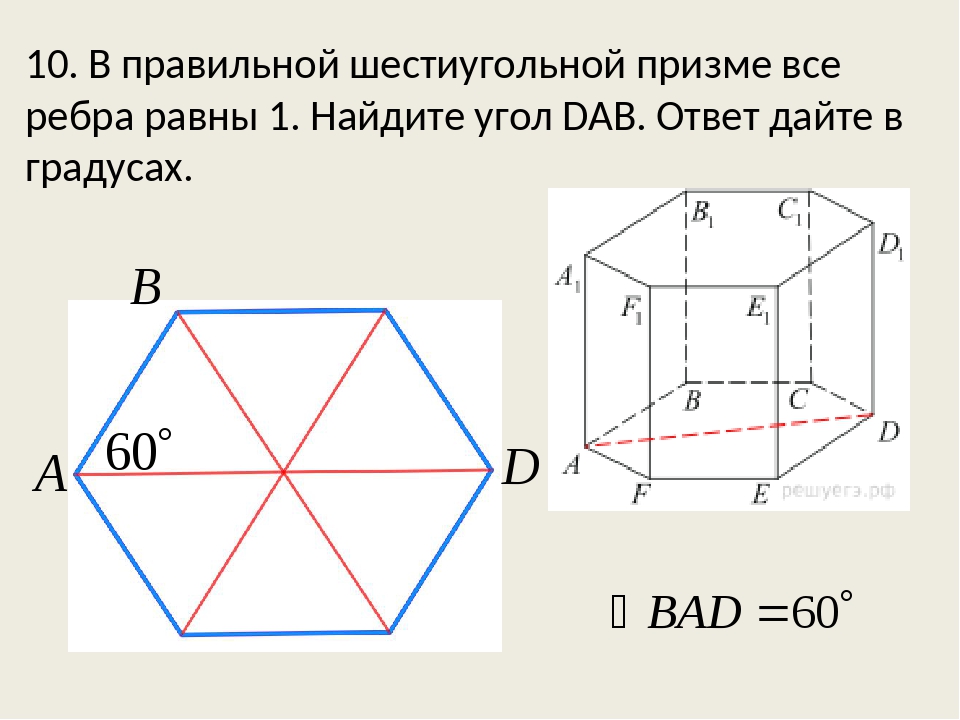
е. более интенсивный и не бледный.
ПОПУТНОЕ ДОПОЛНЕНИЕ К ТЕМЕ. ВОСЬМИУГОЛЬНИКИ по своей форме начинают «округляться» и являются переходным звеном к кругу. Нет доминирующих ударных углов, а центр, в сравнении с шестиугольником, выражен еще более. Правда, внешний контур фигуры пока рациональный, хотя совершенно лишен жесткости. Так что дорожный знак «Движение без остановки запрещено» хоть и в алом цвете, но водителей не раздражает. Тем более что команда «STOP» написана белым, а значит, еще облегчает команду приоритета, психологически снимая агрессивные установки водителей, которые вынуждены остановиться. Как говорится, «стали, подождали, а дальше все опять будет». И еще один очень важный момент относительно восьмиугольника. У этой фигуры резко ослаблена тенденция создавать ячеистые структуры. Это, скорее всего, будет монофирма со своей внутренней идеологией и уравновешенной деловой коммуникацией с партнерами. Удачно для логотипа, если бы только не прочно сложившаяся ассоциация с упомянутым дорожным знаком.
чем он интересен и как его построить
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1.
Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность .
Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонта
Полигоны
Многоугольник — это плоская форма с прямыми сторонами.
Это многоугольник?
Многоугольники — это двумерные фигуры. Они состоят из прямых линий, а форма «замкнута» (все линии соединяются).
| Многоугольник (прямые стороны) | Не Полигон (с изгибом) | Не Полигон (открытый, не закрытый) |
Многоугольник происходит от греческого языка.
Poly- означает «много», а -угольник означает «угол».
Типы полигонов
Обычное или нестандартное
Правильный многоугольник имеет все углы и все стороны равны, в противном случае это неправильный многоугольник
| Обычный | Нерегулярное |
вогнутый или выпуклый
Выпуклый многоугольник не имеет углов, направленных внутрь.Точнее, внутренний угол не может быть больше 180 °.
Если какой-либо внутренний угол больше 180 °, то многоугольник будет вогнутым . ( Подумайте: в вогнутой части есть «пещера» )
| Выпуклая | Вогнутая |
Простой или сложный
Простой многоугольник имеет только одну границу и не пересекает себя.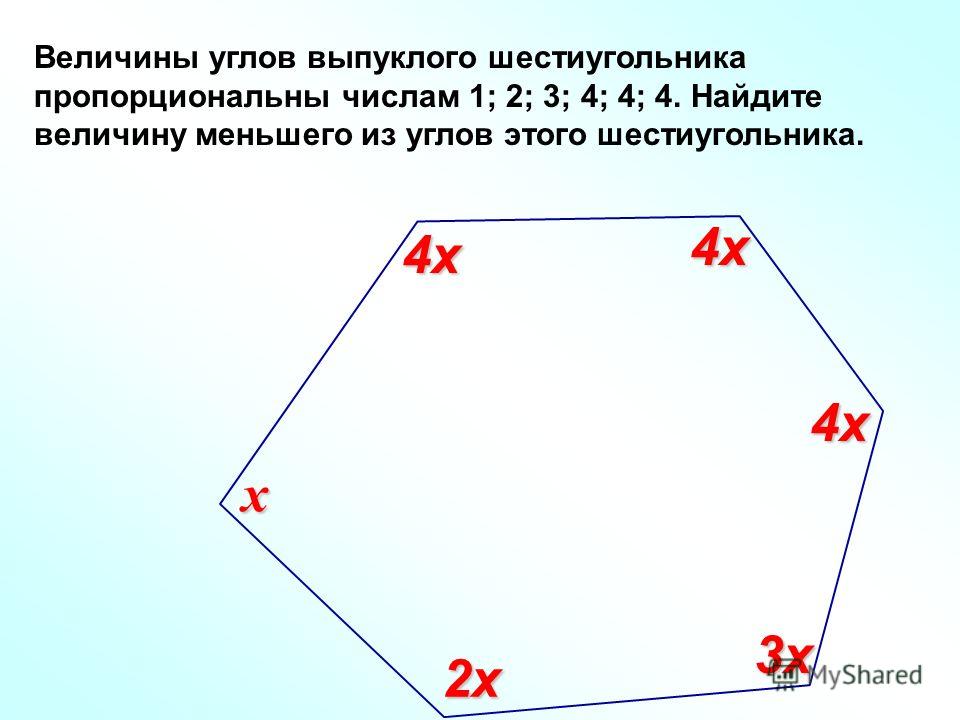
Сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложные.
| Простой многоугольник (это Пентагон) | Сложный многоугольник (также Пентагон) |
Другие примеры
| Шестигранник неправильной формы | Вогнутый восьмиугольник | Сложный многоугольник («звездообразный многоугольник», в данном случае пентаграмма) |
Играй с ними!
Попробуйте интерактивные многоугольники… сделать их правильными, вогнутыми или сложными.
Имена полигонов
С помощью этого метода можно делать имена:
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример: 62-сторонний многоугольник — это гексаконтадигон | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
..
Д. НО, для многоугольников с 13 или более сторонами, это нормально (и проще)
Измерения 5 внутренних углов шестиугольника: 130, 120 °, 80. 160 и 155 Какова мера наибольший внешний угол?
160 и 155 Какова мера наибольший внешний угол? Наука
- Анатомия и физиология
- Астрономия
- Астрофизика
- Биология
- Химия
- науки о Земле
- Наука об окружающей среде
Геометрия | математика | Britannica
Самые ранние известные однозначные примеры письменных записей — датируемые Египтом и Месопотамией около 3100 г.
до н.э. — демонстрируют, что древние народы уже начали разрабатывать математические правила и методы, полезные для съемки земельных участков, строительства зданий и измерения контейнеров для хранения.Начиная примерно с VI века до нашей эры, греки собрали и расширили эти практические знания и на их основе обобщили абстрактный предмет, ныне известный как геометрия, из сочетания греческих слов geo («Земля») и metron («мера»). ) для измерения Земли.
В дополнение к описанию некоторых достижений древних греков, в частности, логического развития геометрии Евклидом в Elements , эта статья исследует некоторые применения геометрии в астрономии, картографии и живописи от классической Греции до средневекового ислама и Европы эпохи Возрождения. .Он завершается кратким обсуждением расширений неевклидовой и многомерной геометрии в современную эпоху.
Древняя геометрия: практическая и эмпирическая
Происхождение геометрии лежит в повседневной жизни.
Традиционный отчет, сохраненный в «Истории » Геродота (V век до н. Э.), Приписывает египтянам изобретение геодезии с целью восстановления стоимости собственности после ежегодного разлива Нила. Точно так же стремление узнать объемы твердых цифр проистекает из необходимости оценивать дань, хранить нефть и зерно и строить плотины и пирамиды.Даже три сложные геометрические задачи древних времен — удвоение куба, разрезание угла и квадрат круга, которые будут обсуждаться позже, — вероятно, возникли из практических вопросов, из религиозных ритуалов, хронометража и строительства, соответственно, в догреческие общества Средиземноморья. И главный предмет поздней греческой геометрии, теория конических сечений, обязана своим общим значением, а, возможно, и своим происхождением, своим приложением к оптике и астрономии.
В то время как многие древние люди, известные и неизвестные, внесли свой вклад в эту тему, ни один из них не сравнится с влиянием Евклида и его Элементов геометрии, книги, которой сейчас 2300 лет и которая является объектом столь же болезненного и кропотливого изучения, как Библия.
Однако об Евклиде известно гораздо меньше, чем о Моисее. Фактически, единственное, что известно с достаточной степенью уверенности, — это то, что Евклид преподавал в Александрийской библиотеке во время правления Птолемея I (323–285 / 283 гг. До н. Э.). Евклид писал не только по геометрии, но также по астрономии и оптике, а также, возможно, по механике и музыке. Только Elements , который был широко скопирован и переведен, уцелел.
Евклид Элементы был настолько полным и ясно написанным, что буквально стер с лица земли работы его предшественников.То, что известно о греческой геометрии до него, происходит главным образом из отрывков, цитируемых Платоном и Аристотелем, а также более поздними математиками и комментаторами. Среди других ценных вещей, которые они сохранили, — некоторые результаты и общий подход Пифагора ( c. 580– c. 905 10 500 до н. Э.) И его последователей. Пифагорейцы убедили себя, что все вещи являются числами или обязаны своим отношением к числам.
Доктрина придавала математике первостепенное значение в исследовании и понимании мира.Платон развивал аналогичную точку зрения, и философы, находившиеся под влиянием Пифагора или Платона, часто восторженно писали о геометрии как о ключах к интерпретации Вселенной. Таким образом, древняя геометрия приобрела ассоциацию с возвышенным, чтобы дополнить ее земное происхождение и репутацию образца точного рассуждения.
Нахождение прямого угла
Древние строители и геодезисты должны были уметь строить прямые углы в поле по запросу. Метод, применявшийся египтянами, принес им в Греции прозвище «съемники каната», по-видимому, потому, что они использовали веревку для составления инструкций по строительству.Один из способов, которым они могли использовать веревку для построения прямоугольных треугольников, заключался в том, чтобы пометить веревку с петлей с узлами, чтобы веревка, удерживая ее за узлы и сильно натянув, образовывала прямоугольный треугольник. Самый простой способ выполнить трюк — взять веревку длиной 12 единиц, завязать узел на 3 единицы с одного конца и еще 5 единиц с другого конца, а затем связать концы вместе, чтобы образовать петлю, как показано на анимация.
Однако египетские писцы не оставили нам инструкций по этим процедурам, а тем более намеков на то, что они знали, как их обобщить, чтобы получить теорему Пифагора: квадрат на прямой напротив прямого угла равен сумме квадратов на двух других. стороны.Точно так же ведические писания древней Индии содержат разделы, называемые sulvasutra s, или «правила веревки», для точного расположения жертвенных алтарей. Необходимые прямые углы были образованы веревками, отмеченными для получения триад (3, 4, 5) и (5, 12, 13).
В вавилонских глиняных табличках ( c. 1700–1500 до н. Э.) Современные историки обнаружили проблемы, решения которых указывают на то, что теорема Пифагора и некоторые особые триады были известны более чем за тысячу лет до Евклида.Однако у прямоугольного треугольника, созданного наугад, очень маловероятно, что все его стороны будут измеряться одной и той же единицей измерения, то есть, каждая сторона будет целым числом, кратным некоторой общей единице измерения.
Этот факт, который был шокирован пифагорейцами, породил концепцию и теорию несоизмеримости.
Поиск недоступного
Согласно древней традиции, Фалес Милетский, живший до Пифагора в VI веке до нашей эры, изобрел способ измерения недоступных высот, таких как египетские пирамиды.Хотя ни одно из его сочинений не сохранилось, Фалес, возможно, хорошо знал о вавилонском наблюдении, что для одинаковых треугольников (треугольников, имеющих одинаковую форму, но не обязательно одинаковый размер) длина каждой соответствующей стороны увеличивается (или уменьшается) на одно и то же число. Определение высоты башни с помощью подобных треугольников показано на рисунке. Древние китайцы достигли измерения недоступных высот и расстояний другим путем, используя «дополнительные» прямоугольники, как показано на следующем рисунке, который дает результаты, эквивалентные результатам греческого метода с использованием треугольников.
Сравнение китайской и греческой геометрических теорем На рисунке показана эквивалентность китайской теоремы о дополнительных прямоугольниках и греческой теоремы о подобных треугольниках.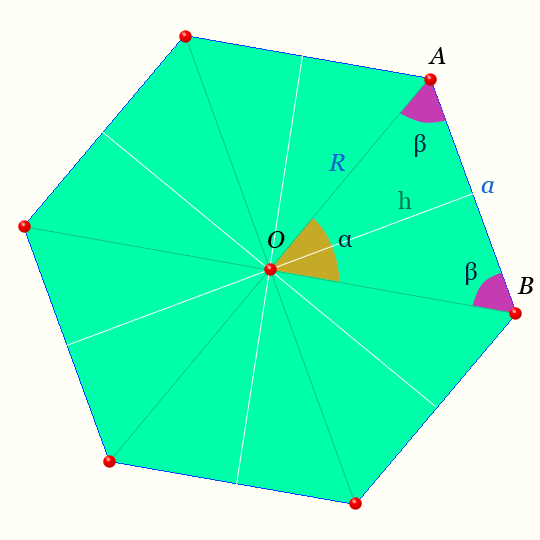
Оценка богатства
Вавилонская клинопись, написанная около 3500 лет назад, посвящена проблемам плотин, колодцев, водяных часов и раскопок. В нем также есть упражнение на круглых ограждениях с предполагаемым значением π = 3. Подрядчик по плавательному бассейну царя Соломона, который сделал пруд 10 локтей в поперечнике и 30 локтей вокруг (3 Царств 7:23), использовал то же значение.Однако евреям следовало взять π у египтян до того, как пересечь Красное море, так как папирус Ринда ( c. 2000 до н.э .; наш основной источник древнеегипетской математики) подразумевает π = 3,1605.
Знание площади круга имело практическую ценность для чиновников, следивших за дани фараона, а также для строителей алтарей и бассейнов. Ахмес, писец, который скопировал и комментировал папирус Райнда ( c. 1650 до н.э.), много говорит о цилиндрических зернохранилищах и пирамидах, целых и усеченных.Он мог вычислить их объемы, и, как видно из его использования египетского секед , горизонтального расстояния, связанного с вертикальным подъемом в один локоть, в качестве определяющей величины для наклона пирамиды, он кое-что знал о подобных треугольниках.