Построение правильных многоугольников — Техническое черчение
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
|
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника. |
Как вписать шестигранник в окружность — Moy-Instrument.Ru
Техническое черчение
Popular
Основы черчения
Строительное
Машиностроительное

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
 Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.
Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Как вписать правильный шестиугольник в окружность
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.

Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA , OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
Полупериметр правильного шестиугольника
Центральный угол правильного шестиугольника в радианах
Центральный угол правильного шестиугольника в градусах
Половина внутреннего угла правильного шестиугольника в радианах
Половина внутреннего угла правильного шестиугольника в градусах
Внутренний угол правильного шестиугольника в радианах
Внутренний угол правильного шестиугольника в градусах
Площадь правильного шестиугольника
Отсюда получим апофему правильного шестиугольника
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Первый способ построения пятиугольника

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Второй способ построения пятиугольника

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N1, Р1, Q1, К1 и соединяем их прямыми.
Третий способ построения пятиугольника

На рисунке построен шестиугольник по данной стороне.
Построение шестиугольника

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов

Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…

Прямой угол, т. е. равный 90°, образуется двумя взаимно перпендикулярными линиями. Перпендикуляр строится следующим образом. Опустить перпендикуляр. Из данной точки С (лежащей вне прямой), как из центра, произвольным радиусом описываем дугу так, чтобы она пересекла данную прямую в двух точках D и Е из этих точек, как из центров, одинаковыми радиусами описываем дуги, чтобы они…

Построение угла, равного данному Угол, равный данному, строится следующим образом. Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…

Деление прямых линий и углов может быть произведено двояким образом: на глаз и с помощью геометрического построения. При делении прямой на две равные части поступают следующим образом. Половину данной прямой берут циркулем на глаз и откладывают эту половину от обоих концов прямой. Если концы половинок сходятся, то, значит, данная прямая разделена правильно, если нет, то…

Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…
§ 79. Вписанный правильный шестиугольник
Чтобы найти способ вписать в данный круг правильный шестиугольник, определим сначала длину его стороны, считая радиус круга известным. Пусть АВ (черт. 219) есть сторона правильного вписанного шестиугольника. Соединим вершины А и В с центром О круга. Так как дуга А и В составляет 6-ю часть полной окружности, то она содержит 360°/6= 60°; столько же градусов заключает центральный угол АОВ . Но если угол при вершине равнобедренного треугольника равен 60°, то углы при основании также равны 60° (почему?). Следовательно, треугольник АОВ – равносторонний: АВ = АО = ВО .

Другими словами, сторона правильного вписанного шестиугольника равна радиусу круга.
Отсюда вытекает способ вписать в круг правильный шестиугольник: надо растворить циркуль на величину радиуса и засечь вдоль окружности шесть раз, а затем соединить точки деления, прямыми линиями.
Scisne ?


Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.

Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку
Все углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — , что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.

Пчелиные соты показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.

Некоторые сложные кристаллы и молекулы , например графит, имеют гексагональную кристаллическую решётку.

Снежинки образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.

Гигантский гексагон — атмосферное явление на Сатурне.

Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Дорога гигантов — памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.

Игровое поле зачастую составляют шестиугольники. Замощение плоскости правильными шестиугольниками является основой для гекса, гексагональных шахмат и других игр на клетчатом поле, полигексов, вариантов модели «Жизнь» и других двумерных клеточных автоматов, кольцевых флексагонов и т.п.

Сечение гайки имеет вид правильного шестиугольника.

Звезда Давида (гексаграмма) — шестиконечная звезда, образованная двумя правильными треугольниками, символ иудаизма.
Шестиугольник — Hexagon — qaz.wiki
Форма с несколькими сторонами
В геометрии , A шестиугольник (от греческой ЕЕ гекса , «шесть» и γωνία, Gonia , «угол, угол») представляет собой шестигранный многоугольник или 6-угольник. Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.
Правильный шестиугольник
Регулярный шестиугольник имеет символ шлефли {6} , а также может быть выполнен в виде усеченного равностороннего треугольника , т {3}, который чередует два типа ребер.

 Когда задана длина стороны AB , вы рисуете вокруг точки A и вокруг точки B дугу окружности. Пересечение М является центром окружности . Перенесите отрезок AB четыре раза на описанную окружность и соедините угловые точки.
Когда задана длина стороны AB , вы рисуете вокруг точки A и вокруг точки B дугу окружности. Пересечение М является центром окружности . Перенесите отрезок AB четыре раза на описанную окружность и соедините угловые точки.Правильный шестиугольник определяется как шестиугольник, который одновременно является равносторонним и равноугольным . Он бицентрический , что означает, что он является как циклическим (имеет описанную окружность), так и касательным (имеет вписанную окружность).
Общая длина сторон равна радиусу окружности или окружности , которая равна раз превышает апофемой (радиус вписанной окружности ). Все внутренние углы составляют 120 градусов . Правильный шестиугольник имеет шесть симметрий вращения ( вращательная симметрия шестого порядка ) и шесть симметрий отражения ( шесть линий симметрии ), составляющих группу диэдра D 6 . Самые длинные диагонали правильного шестиугольника, соединяющие диаметрально противоположные вершины, вдвое превышают длину одной стороны. Из этого можно видеть, что треугольник с вершиной в центре правильного шестиугольника и одной стороной с шестиугольником является равносторонним , и что правильный шестиугольник можно разделить на шесть равносторонних треугольников. 23{\ displaystyle {\ tfrac {2} {\ sqrt {3}}}}
Подобно квадратам и равносторонним треугольникам , правильные шестиугольники подходят друг к другу без каких-либо зазоров для мозаики плоскости (три шестиугольника, сходящиеся в каждой вершине), и поэтому полезны для построения мозаики . Ячейки соты улья шестиугольные по этой причине, а также потому, что форма позволяет эффективно использовать пространство и строительные материалы. Диаграмма Вороного регулярной треугольной решетки является сотовая тесселяция из шестиугольников. Обычно не считается триамбусом , хотя он равносторонний.
Параметры

Максимальный диаметр (который соответствует длинной диагонали шестиугольника), D , в два раза превышает радиус максимальной или описанной окружности , R , которая равна длине боковой, т . Минимальный диаметр или диаметр вписанной окружности (разделение параллельных сторон, расстояние между плоскостями, короткая диагональ или высота при опоре на плоское основание), d , в два раза больше минимального радиуса или inradius , r . Максимумы и минимумы связаны одним и тем же фактором:
- 12dзнак равнорзнак равнопотому что(30∘)рзнак равно32рзнак равно32т{\ displaystyle {\ frac {1} {2}} d = r = \ cos (30 ^ {\ circ}) R = {\ frac {\ sqrt {3}} {2}} R = {\ frac {\ sqrt {3}} {2}} t} и аналогично dзнак равно32D.{\ displaystyle d = {\ frac {\ sqrt {3}} {2}} D.}
Площадь правильного шестиугольника
- Азнак равно332р2знак равно3ррзнак равно23р2знак равно338D2знак равно34Ddзнак равно32d2≈2,598р2≈3,464р2≈0,6495D2≈0,866d2.{\ displaystyle {\ begin {align} A & = {\ frac {3 {\ sqrt {3}}} {2}} R ^ {2} = 3Rr = 2 {\ sqrt {3}} r ^ {2} \ \ & = {\ frac {3 {\ sqrt {3}}} {8}} D ^ {2} = {\ frac {3} {4}} Dd = {\ frac {\ sqrt {3}} {2 }} d ^ {2} \\ & \ приблизительно 2,598R ^ {2} \ приблизительно 3,464r ^ {2} \\ & \ приблизительно 0,6495D ^ {2} \ приблизительно 0,866d ^ {2}. \ end {выровнено }}}
Для любого правильного многоугольника площадь также можно выразить через апофему a и периметр p . Для правильного шестиугольника они даются как a = r и p , поэтому знак равно6рзнак равно4р3{\ displaystyle {} = 6R = 4r {\ sqrt {3}}}
- Азнак равноап2знак равнор⋅4р32знак равно2р23≈3,464р2.{\ displaystyle {\ begin {align} A & = {\ frac {ap} {2}} \\ & = {\ frac {r \ cdot 4r {\ sqrt {3}}} {2}} = 2r ^ {2 } {\ sqrt {3}} \\ & \ приблизительно 3,464r ^ {2}. \ end {align}}}
Правильный шестиугольник заполняет часть его окружности . 332π≈0,8270{\ displaystyle {\ tfrac {3 {\ sqrt {3}}} {2 \ pi}} \ приблизительно 0,8270}
Если правильный шестиугольник имеет последовательные вершины A, B, C, D, E, F и если P — любая точка на описанной окружности между B и C, то PE + PF = PA + PB + PC + PD .
Из отношения радиуса описанной окружности к внутреннему радиусу следует, что отношение высоты к ширине правильного шестиугольника составляет 1: 1,1547005; то есть шестиугольник с длинной диагональю 1,0000000 будет иметь расстояние 0,8660254 между параллельными сторонами.
Точка в плоскости
Для произвольной точки на плоскости правильного шестиугольника с описанным радиусом , расстояния до центра тяжести правильного шестиугольника и его шести вершин равны и соответственно, имеем р{\ displaystyle R}L{\ displaystyle L}dя{\ displaystyle d_ {i}}
- d12+d42знак равноd22+d52знак равноd32+d62знак равно2(р2+L2),{\ displaystyle d_ {1} ^ {2} + d_ {4} ^ {2} = d_ {2} ^ {2} + d_ {5} ^ {2} = d_ {3} ^ {2} + d_ { 6} ^ {2} = 2 (R ^ {2} + L ^ {2}),}
- d12+d32+d52знак равноd22+d42+d62знак равно3(р2+L2),{\ displaystyle d_ {1} ^ {2} + d_ {3} ^ {2} + d_ {5} ^ {2} = d_ {2} ^ {2} + d_ {4} ^ {2} + d_ { 6} ^ {2} = 3 (R ^ {2} + L ^ {2}),}
- d14+d34+d54знак равноd24+d44+d64знак равно3((р2+L2)2+2р2L2).{\ displaystyle d_ {1} ^ {4} + d_ {3} ^ {4} + d_ {5} ^ {4} = d_ {2} ^ {4} + d_ {4} ^ {4} + d_ { 6} ^ {4} = 3 ((R ^ {2} + L ^ {2}) ^ {2} + 2R ^ {2} L ^ {2}).}
Если — расстояния от вершин правильного шестиугольника до любой точки его описанной окружности, то dя{\ displaystyle d_ {i}}
- (∑язнак равно16dя2)2знак равно4∑язнак равно16dя4.{\ Displaystyle (\ сумма _ {я = 1} ^ {6} d_ {я} ^ {2}) ^ {2} = 4 \ сумма _ {я = 1} ^ {6} d_ {я} ^ {4 }.}
Симметрия
 Шесть линий отражения правильного шестиугольника с симметрией Dih 6 или r12 , порядок 12.
Шесть линий отражения правильного шестиугольника с симметрией Dih 6 или r12 , порядок 12.  Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров). Циклические симметрии в среднем столбце помечены как g для их центральных порядков вращения. Полная симметрия регулярной формы равна r12, а симметрия не помечена как a1 .
Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров). Циклические симметрии в среднем столбце помечены как g для их центральных порядков вращения. Полная симметрия регулярной формы равна r12, а симметрия не помечена как a1 .Правильный шестиугольник имеет DIH 6 симметрии, порядок 12. Есть три подгруппы: двугранная DIH 3 , DIH 2 и DIH 1 , и четыре циклических подгрупп: Z 6 , Z 3 , Z 2 и Z 1 .
Эти симметрии выражают девять различных симметрий правильного шестиугольника. Джон Конвей помечает их буквой и групповым порядком. r12 — полная симметрия, а a1 — несимметрия. p6 , изогональный шестиугольник, построенный из трех зеркал, может чередовать длинные и короткие края, и d6 , изотоксальный шестиугольник, построенный с равной длиной ребер, но вершинами, чередующимися с двумя разными внутренними углами. Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного шестиугольника. В i4 формы правильные шестиугольники уплощены или растягиваются вдоль одного направления симметрии. Его можно рассматривать как удлиненный ромб , а d2 и p2 можно рассматривать как вытянутые по горизонтали и вертикали воздушные змеи . Шестиугольники g2 , противоположные стороны которых параллельны, также называются шестиугольными параллелогонами .
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g6 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .
| Пример шестиугольников по симметрии |
|---|
Шестиугольники симметрии g2 , i4 и r12 , как параллелогоны, могут разбить евклидову плоскость путем сдвига. Другие формы шестиугольника могут перекрывать плоскость с разной ориентацией.
Группы A2 и G2
Шесть корней простой группы Ли A2 , представленной диаграммой Дынкина 

 , имеют правильный шестиугольный узор. Угол между двумя простыми корнями составляет 120 °.
, имеют правильный шестиугольный узор. Угол между двумя простыми корнями составляет 120 °.
12 корней исключительной группы Ли G2 , представленной диаграммой Дынкина 

 также имеют шестиугольную форму. Два простых корня двух длин имеют угол между собой 150 °.
также имеют шестиугольную форму. Два простых корня двух длин имеют угол между собой 150 °.
Рассечение
Кокстеровские гласит , что каждый зоногон (2 м -угольник которого противоположные стороны параллельны и равны по длине) можно разрезать на м ( м -1) / 2 параллелограммов. В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Это разложение правильного шестиугольника основано на многоугольной проекции куба Петри с 3 из 6 квадратных граней. Остальные параллелогоны и проективные направления куба рассечены прямоугольными кубоидами .
Связанные полигоны и мозаики
На правильном шестиугольнике есть символ Шлефли {6}. Правильный шестиугольник — это часть правильной шестиугольной мозаики {6,3} с тремя шестиугольными гранями вокруг каждой вершины.
Правильный шестиугольник можно также создать как усеченный равносторонний треугольник с символом Шлефли t {3}. При рассмотрении с двумя типами (цветами) кромок эта форма имеет только симметрию D 3 .
Усеченный шестиугольник, т {6}, является двенадцатиугольник , {12}, чередуя два типа (цвета) ребер. Чередовались шестиугольник, ч {6}, представляет собой равносторонний треугольник , {3}. Правильный шестиугольник можно сделать звездообразным с равносторонними треугольниками по краям, образуя гексаграмму . Правильный шестиугольник можно разрезать на шесть равносторонних треугольников , добавив центральную точку. Этот узор повторяется внутри правильной треугольной плитки .
Правильный шестиугольник можно расширить до правильного двенадцатиугольника , добавив чередующиеся квадраты и равносторонние треугольники вокруг него. Этот узор повторяется внутри ромбогексагональной плитки .
Всего шесть самопересекающихся шестиугольников с расположением вершин правильного шестиугольника:
Гексагональные конструкции
Дорога гигантов крупным планомОт пчелиных сот до «Дороги гигантов» в природе преобладают шестиугольные узоры из-за их эффективности. В гексагональной сетке каждая линия настолько коротка, насколько это возможно, если большая область должна быть заполнена наименьшим количеством шестиугольников. Это означает, что для изготовления сот требуется меньше воска, и они приобретают большую прочность при сжатии .
Неправильные шестиугольники с параллельными противоположными краями называются параллелогонами и также могут перекрывать плоскость путем сдвига. В трех измерениях шестиугольные призмы с параллельными противоположными гранями называются параллелоэдрами, и они могут преобразовывать трехмерное пространство в мозаику путем перемещения.
Месселяция шестиугольниками
В дополнение к правильному шестиугольнику, который определяет уникальную мозаику плоскости, любой неправильный шестиугольник, который удовлетворяет критерию Конвея, будет мозаикой плоскости.
Шестиугольник, вписанный в коническое сечение
Теорема Паскаля (также известная как «Теорема Hexagrammum Mysticum») утверждает, что если произвольный шестиугольник вписан в какое-либо коническое сечение и пары противоположных сторон растянуты до тех пор, пока они не встретятся, три точки пер
| Развернуть структуру обучения | Свернуть структуру обучения |
|
Как нарисовать шестиугольник в круге
/
/
Как нарисовать шестиугольник в круге
Popular
Основы черчения
Строительное
Машиностроительное
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и п
Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них
Для треугольника всегда возможны и вписанная окружность и описанная окружность.
Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы. Из всех параллелограммов только в ромб и квадрат можно вписать окружность. Ее центр лежит на пересечении диагоналей.
Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.
Вокруг трапеции возможно описать окружность или в трапецию можно вписать окружность если трапеция равнобокая.
Центр описанной окружности
Теорема. Центр описанной около треугольника окружности является точкой пересечениясерединных перпендикуляров к сторонам треугольника.
Центр описанной около многоугольника окружности является точкой пересечения серединных перпендикуляров к сторонам этого многоугольника.
Центр Вписанная окружность
Определение. Вписанная в выпуклый многоугольник окружность — это окружность, которая касается всех сторон этого многоугольника (то есть каждая из сторон многоугольника является для окружностикасательной).
Центр вписанной окружности лежит внутри многоугольника.
Многоугольник, в который вписана окружность, называется описанным.
В выпуклый многоугольник можно вписать окружность, если биссектрисы всех его внутренних углов пересекаются в одной точке.
Центр вписанной в многоугольник окружности — точка пересечения его биссектрис.
Центр вписанной окружности равноудален от сторон многоугольника. Расстояние от центра до любой стороны равно радиусу вписанной окружности По свойству касательных, проведённых из одной точки, любая вершина описанного многоугольника равноудалена от точек касания, лежащих на сторонах, выходящих из этой вершины.
В любой треугольник можно вписать окружность. Центр вписанной в треугольник окружности называется инцентром.
В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. В частности, в трапецию можно вписать окружность, если сумма её оснований равна сумме боковых сторон.
В любой правильный многоугольник можно вписать окружность. Около любого правильного многоугольника можно также описать окружность. Центр вписанной и описанной окружностей лежат в центре правильного многоугольника.
Для любого описанного многоугольника радиус вписанной окружности может быть найден по формуле
 где S — площадь многоугольника, p — его полупериметр.
где S — площадь многоугольника, p — его полупериметр.
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
1. Формула стороны правильного n-угольника через радиус вписанной окружности:
2. Формула стороны правильного n-угольника через радиус описанной окружности:
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
Правильный треугольник
Формулы правильного треугольника:
1. Формула стороны правильного треугольника через радиус вписанной окружности: a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности: a = R√3
3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
5. Формула площади правильного треугольника через длину стороны:
6. Формула площади правильного треугольника через радиус вписанной окружности: S = r2 3√3
7. Формула площади правильного треугольника через радиус описанной окружности:
8. Угол между сторонами правильного треугольника: α = 60°
Правильный четырехугольнику — квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности: a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности: a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
5. Формула площади правильного четырехугольника через длину стороны: S = a2
6. Формула площади правильного четырехугольника через радиус вписанной окружности: S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности: S = 2 R2
8. Угол между сторонами правильного четырехугольника: α = 90°
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
2. Формула стороны правильного шестиугольника через радиус описанной окружности: a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны: R = a
5. Формула площади правильного шестиугольника через длину стороны:
6. Формула площади правильного шестиугольника через радиус вписанной окружности: S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
8. Угол между сторонами правильного шестиугольника: α = 120°
Значение числа (произносится «пи») — математическая константа, равная отношению
(произносится «пи») — математическая константа, равная отношению
длины окружности к длине её диаметра, оно выражается бесконечной десятичной дробью.
Обозначается буквой греческого алфавита «пи». Чему равно число пи? В простых случаях хватает знать первые 3 знака (3,14).
53. Найдем длину дуги окружности радиуса R, отвечающей центральному углу в n°

Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан. 
Градусная мера угла в 1 радиан равна:
Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е. 
И наоборот 
Так как π = 3,14, то 1 рад = 57,3°
Если угол содержит a радиан, то его градусная мера равна 
И наоборот 
Обычно при обозначении меры угла в радианах наименование «рад» опускают.
Например, 360° = 2π рад, пишут 360° = 2π
В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.
| ПРИМЕЧАНИЕ. Шаги с 1 по 7 такие же, как и для построения шестиугольника, вписанного в круг. В случае вписанного равностороннего треугольника мы используем все остальные точки на окружности. | ||
| 1 | A, B, C, D, E, F все лежат в центре окружности O | По конструкции. |
| 2 | AB = BC = CD = DE = EF | Все они были нарисованы с одинаковой шириной циркуля. |
| Из (2) мы видим, что пять сторон равны по длине, но последняя сторона FA не была нарисована циркулем. Это было «оставшееся» пространство, когда мы обошли круг и остановились у F. Итак, мы должны доказать, что это соответствует остальным пяти сторонам. | ||
| 3 | OAB — равносторонний треугольник | AB был нарисован с шириной компаса, установленной на OA, и OA = OB (оба радиуса круга). |
| 4 | м∠AOB = 60 ° | Все внутренние углы равностороннего треугольника равны 60 °. |
| 5 | м∠AOF = 60 ° | Как и в (4) m∠BOC, m∠COD, m∠DOE, m∠EOF все равны & 60deg; Так как все центральные углы складываются в 360 °, м∠AOF = 360 — 5 (60) |
| 6 | Треугольник BOA, AOF совпадают | SAS См. Тест на соответствие, угол-угол-сторона. |
| 7 | AF = AB | CPCTC — Соответствующие части конгруэнтных треугольников конгруэнтны |
| Итак, теперь мы можем доказать, что BDF — это равносторонний треугольник | ||
| 8 | Все шесть центральных углов (∠AOB, ∠BOC, ∠COD, ∠DOE, ∠EOF, ∠FOA) совпадают. | Из (4) и повторением для других 5 углов все шесть углов имеют меру 60 °. |
| 9 | Углы ∠BOD, ∠DOF, ∠BOF равны | Из (8) — Каждый из них представляет собой сумму двух углов по 60 ° |
| 10 | Треугольники BOD, DOF и BOF совпадают. | Стороны представляют собой равные радиусы окружности, а из (9) включенные углы совпадают. См. Тест на соответствие, сторона-угол-сторона |
| 11 | BDF — равносторонний треугольник. | Из (10) BD, DF, FB конгруэнтно. CPCTC — соответствующие части конгруэнтных треугольников конгруэнтны. Это, в свою очередь, удовлетворяет определению равносторонний треугольник. |
| 12 | BDF — равносторонний треугольник, вписанный в данную окружность | Из (11) и все три вершины B, D, F лежат на данной окружности. |
Как рассчитать диаметр шестиугольника
Хватай свой футбольный мяч, пора заниматься математикой! Хотя уже не в моде, на протяжении десятилетий сферический объект, о котором пинали на чемпионате мира, был сшит из 20 шестиугольников и 12 пятиугольников. Но это не единственный способ узнать этот многоугольник. Чтобы полностью оценить размеры шестиугольника, вы должны признать форму сот, созданных геометрическим гением пчел. Вы знаете, что шестиугольник есть везде, но как его измерить?
Самый простой способ построить правильный шестиугольник — это нарисовать шесть равносторонних треугольников, все из которых имеют общую вершину в центральной точке шестиугольника.
Углы внутреннего шестиугольника в каждой из шести вершин составляют 120 °. Общее количество диагоналей шестиугольника равно девяти. Три из них — длинные диагонали, пересекающие центральную точку, а шесть других также называют «высотой» шестиугольника.
Расчет диаметра шестиугольника
Сначала измерьте все остальные стороны шестиугольника, чтобы убедиться, что шестиугольник правильный. У правильного шестиугольника все шесть сторон будут равны. Если шестиугольник неправильной формы, у него не будет диаметра.
Далее, есть два простых способа рассчитать диаметр шестиугольника.
- Измерьте длину стороны и умножьте ее на 2.
- Умножьте радиус на 2. (Расстояние от пересечения двух сторон до центра называется радиусом.)
Определение площади правильного Шестигранник
- Разделите фигуру на треугольники.
- Вычислите площадь одного треугольника. Помните, чтобы найти площадь треугольника , умножьте основание на высоту, а затем разделите на 2.
- Теперь умножьте это значение на 6.
Измерение углов шестиугольника
Чтобы найти сумму внутренних углов шестиугольника, разделите его на четыре равных треугольника. Поскольку сумма углов каждого треугольника составляет 180 градусов, вы получаете:
4 𝗑 180 ° = 720 °
Таким образом, сумма внутренних углов шестиугольника составляет 720 градусов.
Измерение внутренних углов
Все стороны правильного шестиугольника равны (одинаковой длины), и все внутренние углы также совпадают.Итак, чтобы измерить внутренние углы , вы берете сумму всех углов, которая составляет 720 градусов, и делите ее на количество углов, равное 6.
720 ° ÷ 6 = 120 °
Итак, 720 градусов деленное на 6 равно 120 градусам.
Внутренний угол правильного шестиугольника составляет 120 градусов.
Измерение центрального угла
Сначала нарисуйте круг в середине шестиугольника. Вы знаете, что круг равен 360 градусам. Поэтому все, что вам нужно сделать, это разделить это на шесть углов.
360 ° ÷ на 6 = 60 °
Размер центрального угла правильного шестиугольника составляет 60 градусов.
Калькулятор компоновки шестиугольника может быть полезным инструментом для решения основных вопросов измерения шестиугольника. Дизайнеры, а также плотники часто используют их, чтобы создать идеальный шестиугольник при проектировании и строительстве плиточных полов, стеклянных окон или даже игрового оборудования.
Видео: кадрирование изображения по форме
Используйте инструменты кадрирования в PowerPoint, чтобы обрезать и удалять ненужные части изображений или обрезать изображение по размеру формы.
Обрезка изображения по форме
Если вы хотите изменить контур изображения и придать ему форму (например, круг или звезду), используйте инструменты обрезки на вкладке ИНСТРУМЕНТЫ ИЗОБРАЖЕНИЯ ФОРМАТ .
Выберите изображение (или изображения), которое вы хотите обрезать.
Если вы обрезаете много изображений одновременно, вы должны использовать одну и ту же форму для всех из них.Чтобы обрезать изображения различной формы, кадрируйте каждое изображение по одному
На вкладке ИНСТРУМЕНТЫ ИЗОБРАЖЕНИЯ ФОРМАТ щелкните Обрезать > Обрезать по фигуре , а затем выберите нужную форму.
Обрезать по фигуре или заполнить ее
Вы можете использовать изображение в качестве заливки фигуры. Просто щелкните фигуру, к которой вы хотите добавить изображение, затем в разделе ИНСТРУМЕНТЫ ДЛЯ РИСОВАНИЯ на вкладке ФОРМАТ щелкните Стили фигур > Заливка формы > Изображение и выберите нужный рисунок.
Щелкните изображение, которое вы хотите внутри фигуры.
Щелкните ИНСТРУМЕНТЫ ИЗОБРАЖЕНИЙ > ФОРМАТ > Размер и щелкните стрелку под Обрезать . Если вкладки Работа с изображениями и Формат не отображаются, убедитесь, что вы выбрали изображение.
Нажмите Заполните или Установите .
Заливка устанавливает размер изображения в соответствии с высотой или шириной фигуры, в зависимости от того, что больше. Это заполнит фигуру изображением.
По размеру устанавливает размер изображения так, чтобы высота и ширина изображения соответствовали границам фигуры. Это максимально поместит изображение в форму.Некоторые области фигуры могут остаться пустыми.
Когда вы закончите, нажмите ESC.
Хотите больше?
Обрезать картинку
Вы можете улучшить изображение, придав ему другую форму. Быстрый способ сделать это — использовать Crop to Shape .
Сначала выберите изображение на слайде.
Затем найдите вкладку ИНСТРУМЕНТЫ ИЗОБРАЖЕНИЯ ФОРМАТ , которая появляется при выборе изображения. Щелкните FORMAT .
На вкладке ФОРМАТ в группе Размер щелкните стрелку под Обрезать и укажите на Обрезать до формы .
Откроется галерея фигур, в которой вы можете выбрать форму для изображения.
Найдите форму, которая хорошо сочетается с изображением и ориентацией изображения.Для этого изображения давайте попробуем прямоугольник с закругленными углами.
Эта форма прекрасно работает, вырезая небольшую часть изображения и придавая ему закругленные углы.
Обратите внимание, что Crop to Shape сохраняет соотношение сторон изображения, то есть пропорции его высоты к ширине.
Чтобы поэкспериментировать с другой формой, просто щелкните стрелку под Обрезать и укажите на Обрезать до формы .
Давайте поищем совсем другую форму.Как насчет звезды?
Интересно, но я думаю, что он вырезает слишком много из изображения, особенно из центральной фигуры.
Я нажму Отменить , чтобы вернуться к форме прямоугольника со скругленными углами, которая лучше соответствует этому изображению.
Теперь, когда изображение все еще выбрано и отображается вкладка FORMAT , я немного отформатирую изображение.
Например, я нажимаю Граница изображения и выбираю цвет границы.
Затем я снова нажму Граница изображения , наведу указатель на Толщина и увеличу ширину границы до 4 ½ пункта, чтобы она была более заметной.
Это приятный простой акцент.
Если вам нужно более сложное форматирование изображения, вот быстрый способ его применить и использовать Обрезать по форме .
Вернемся к исходной картинке.
На этот раз, прежде чем использовать Обрезать по фигуре , я выделю изображение, нажмите ФОРМАТ и нажмите Еще , чтобы открыть галерею стилей изображения .
Стили галереи сочетают в себе разные вещи — тип формы изображения, цвета и стили границ, а также такие эффекты, как отражения и тени.
Я найду стиль изображения, который мне нравится, например этот, с белой рамкой и тенью в перспективе, и щелкните, чтобы применить его.
Затем, не снимая выделения с изображения, я нажимаю стрелку Crop , указываю на Crop to Shape и выбираю прямоугольник с закругленными углами.
После этого процесса я быстро получил более сложный стиль изображения, затем я выбрал желаемую форму, используя Crop to Shape .
Для получения дополнительных сведений см. Краткое содержание курса и поэкспериментируйте с PowerPoint.
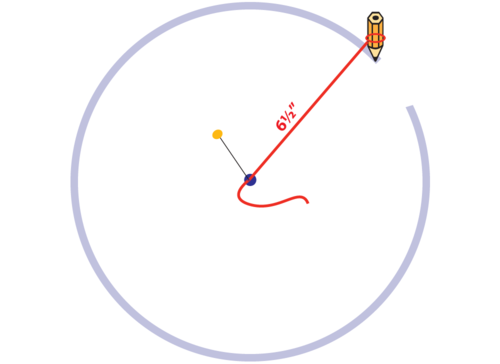
Как нарисовать и измерить круг без шаблона

Круг, по моему скромному мнению, королева геометрических форм. Не поймите меня неправильно; Мне нравятся все эти квадраты, прямоугольники, треугольники, восьмиугольники и еще много чего; но круг — самый крутой из всех: гладкий, красивый и бесконечно полезный. Однако попытаться нарисовать идеальный круг без узора — непростая задача, а определение правильного размера отверстия, в которое можно вставить круг, требует работы с числом Пи (или π), а это не тот вкусный вид, с которым можно есть. немного мороженого.Мы здесь сегодня, чтобы помочь вам с шагами, которые вы забыли с урока геометрии в средней школе (или, может быть, никогда не выучили, потому что вы были слишком заняты передачей заметок со Сьюзен Эллери!) . Мы покажем вам части круга, какой ширины отрезать ткань, чтобы она соответствовала кругу, и как нарисовать круг без рисунка. Мы также включили удобное преобразование десятичных знаков в дюймы, которое необходимо при работе с числом Пи.
Давайте начнем с запоминания того, как называются все части круга, и как число Пи (π) вписывается в эту смесь.
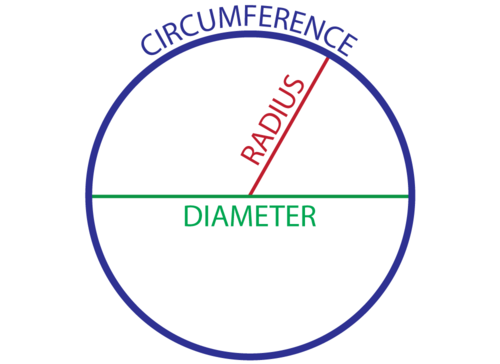
Радиус : расстояние от центра круга до внешнего края
Диаметр : расстояние по окружности через его центральную точку
Окружность : расстояние по внешнему краю окружности
π или Пи: имя, данное отношению длины окружности круга к его диаметру, выраженное десятичной дробью 3,14
Если вам известен диаметр вашего круга, вы можете использовать стандартную формулу, чтобы вычислить ширину отрезка ткани, необходимого для изготовления трубки.Эта ширина равна окружности круга, который будет вставлен в трубку (у нас есть отличное пошаговое руководство о том, как вставить круг в трубку).
Формула: 3,14 (π) x диаметр = окружность
Пример: Вам нужна готовая основа диаметром 12 дюймов (круг диаметром 12 дюймов) в спортивной сумке.
3,14 x 12 дюймов = 37,68 дюймов
(Это также работает с метрической системой: 3.14 x 30 см = 94,2 см)
Важный шаг, который многие люди упускают на этом этапе, — это забыть добавить (к обеим частям) припуск на шов. Если вы используете стандартный припуск на шов ½ дюйма, вам нужно добавить 1 дюйм к диаметру вашего круга (диаметр увеличивается вдвое над припуском на шов) и на 1 дюйм к ширине вашей ткани ( ½ дюйма для обеих сторон припуска на шов). В нашем примере это означает:
Круг должен начинаться с диаметра 13 дюймов.
Ткань должна быть шириной 38,68 дюйма
Высота кроя ткани варьируется и зависит от вашего проекта. Например, высокая спортивная сумка может быть 30 дюймов в высоту, а более короткое ведро — всего 10 дюймов.

Если вы используете Пи, помните, что он всегда возвращает десятичное число. Если вы уже имеете дело с метрической системой, то ничего страшного — конвертация не требуется.
Для тех из нас, кто работает в мире дюймов, вам нужно найти преобразование в метры.
В нашем примере у нас 38,68 дюйма. Харумф! Приведенная ниже таблица даст вам достаточно точное совпадение линейки.
Десятичное число 0,68 ближе всего к 0,63 или ». Мы можем использовать 38 ”в качестве ширины куска ткани, который вы режете для трубки.

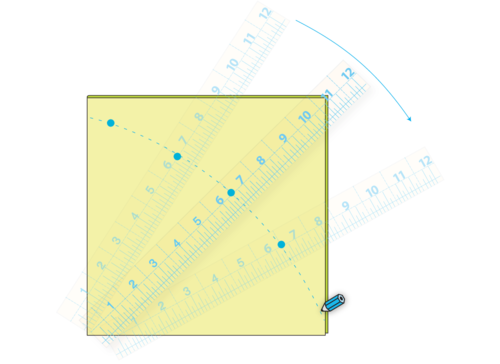
Если у вас есть запасные компасы, вам повезло, и вы легко можете нарисовать себе круги любого размера. Но вы также можете легко сделать свой собственный циркуль, чтобы нарисовать круг.
Для начала вам нужно знать, какого размера вы хотите получить круг (диаметр).В нашем текущем примере нам нужна окружность диаметром 13 дюймов
Чтобы нарисовать круг, вам нужно знать его радиус. Как вы узнали выше в первом разделе, радиус составляет половину диаметра. В нашем примере половина 13 дюймов равна 6½ дюйма.
Метод полного круга
- Используйте лист легкой бумаги (хорошо подойдет бумага для миллиметров или шаблонов), размер которой по крайней мере на 1 дюйм больше, чем круг, который вы хотите нарисовать.
- Отрежьте кусок веревки примерно на 4–5 дюймов длиннее вашего радиуса.Мы использовали веревку длиной 10 дюймов.
- Привяжите один конец бечевки к короткому карандашу.
- Поместите конец карандаша по направлению к внешнему краю бумаги, оставив достаточно места от края, чтобы сделать полный проход.
- Измерьте длину радиуса (в данном случае 6½ дюймов) от места, где конец карандаша касается бумаги назад.
- Приколите шнур прямо к бумаге именно в этом месте.
- Натягивая веревку, нарисуйте идеальный круг с помощью самодельного циркуля.

Метод сложенных четвертинок
- Опять же, начните с квадрата из тонкой бумаги не менее чем на 1 дюйм больше круга, который вы хотите нарисовать.
- Сложите бумагу пополам. Убедитесь, что ваш оригинальный квадрат ровный и правдивый! Расположите бумагу загнутыми краями по нижнему и левому краям, а открытыми краями — по верхнему и правому краям.
- Поместите прозрачную линейку точно в центр левого нижнего угла сложенного квадрата. Поверните линейку сверху вниз квадрата, как маятник или циркуль, измеряя и отмечая точку в точке 6½ дюйма в трех-четырех точках.Вы создаете полукруглую дугу. Убедитесь, что конец линейки в угловой точке не смещается.

- Прорежьте по дуге все слои и разверните готовый круг диаметром 13 дюймов. Теперь вы можете использовать этот узор из бумаги, чтобы вырезать круг из ткани.
Теперь вы можете сшить боковой шов основного кроя ткани с помощью нового элегантного кружка. Затем приколите основу к получившейся трубке и пришейте трубку к кругу с припуском на шов ½ дюйма. В результате получилось готовое основание диаметром 12 дюймов.
Как упоминалось выше, для получения дополнительной информации об этой технике см. Наше руководство: Как вставить плоский круг в трубку.
Решено: как оптическая иллюзия превращает круги в шестиугольники
Когда вы смотрите на красочное изображение, а затем поворачиваетесь, чтобы посмотреть на нейтральный фон, появляется «фантомное изображение» контрастных цветов. Теперь новое исследование обнаруживает, что похожая иллюзия возникает с формами, превращающими круги в шестиугольники и наоборот.
Эти два визуальных явления имеют разные причины, хотя и похожи.В то время как цветная оптическая иллюзия возникает из-за утомленных светочувствительных клеток глаза, иллюзия остаточного изображения формы возникает из-за зрительных частей мозга, сказал исследователь Хироюки Ито из Университета Кюсю в Японии.
«Остаточные изображения обычно незаметны или размыты», — написал Ито в электронном письме LiveScience. Но для ученых изображения могут дать соблазнительные подсказки о том, что происходит в мозгу.
Круг или шестиугольник?
Визуальный эффект, при котором один цвет становится другим в остаточных изображениях, хорошо известен и понятен.Это происходит, когда светочувствительные клетки глаза адаптируются и теряют чувствительность, посылая в мозг сигналы, идентичные сигналам, которые были бы отправлены, если бы вы смотрели на противоположный цвет.
Однако мало кто замечает, что форма, которую они видят в остаточном изображении, может быть не той, на которую они смотрели в реальной жизни.
Ито обнаружил, что когда участники исследования смотрели на круги или шестиугольники в течение 10 секунд, а затем смотрели на серый фон, те, кто смотрел на круги, почти всегда видели остаточное изображение шестиугольников.Точно так же участники, которые смотрели на шестиугольники, очень часто видели круглые остаточные изображения. (Вы можете попробовать это здесь.)
Ито провел серию экспериментов с очерченными и закрашенными шестиугольниками и кругами, которые были как неподвижными, так и вращающимися. В каждом случае добровольцев просили сосредоточиться на черном кресте, окруженном шестиугольниками или кругами на экране компьютера. Через 10 секунд появился серый фон, на который их мозг наложил остаточное изображение. Наблюдателей попросили сообщить, какие из семи форм — включая треугольники, квадраты, шестиугольники и додекагоны — больше всего напоминают остаточные изображения.
Ито обнаружил, что иллюзия была последовательной: некоторые люди даже начинали наблюдать переход, когда смотрели на формы, видя, как круги превращаются в шестиугольники и наоборот.
Но эти открытия не объяснили, почему существует иллюзия. Цветные остаточные изображения возникают в глазу после того, как клетки сетчатки адаптируются и теряют чувствительность к цвету, на который вы смотрели. Если вы смотрите на красную точку только правым глазом, остаточное изображение появится только в этом глазу, а не в левом.
Если в глазу возникают остаточные изображения формы, то же самое явление для правого и левого глаза должно быть справедливо для видения шестиугольников и кругов. Ито организовал эксперименты с компьютерными мониторами и зеркалами так, чтобы участники видели разные изображения правым и левым глазом. Во всех случаях изображение, направленное в правый глаз, представляло собой шесть неподвижных кругов. Изображение для левого глаза изменилось: одни люди видели неподвижные круги, другие вращающиеся круги, вращающиеся звезды или вращающиеся шестиугольники. После фиксации изображения добровольцы сообщили, какую форму остаточного изображения они видели в своем правом глазу.[Удивительные оптические иллюзии]
Все в уме
Результаты показали, что остаточные изображения правого глаза участников менялись вместе с тем, что видел левый глаз. Например, когда левый глаз сфокусировался на вращающихся кругах, респонденты сообщили, что правый глаз видел остаточные изображения углового шестиугольника. Но когда левый глаз видел вращающиеся шестиугольники, правый глаз видел круглые остаточные изображения.
Если бы остаточные изображения формы были вызваны сетчаткой, вид для правого глаза не изменился бы вместе с левым.Это, по словам Ито, предполагает, что иллюзия возникает в области обработки изображений мозга. Результаты будут опубликованы в январе в журнале Psychological Science Ассоциации психологической науки (APS).
Точные виновники не определены, сказал Ито, но, скорее всего, это работает следующим образом: определенные клетки мозга реагируют на изгибы, углы или и то, и другое. Чтобы предотвратить двоение в глазах, криволинейные и угловые ячейки, вероятно, подавляют друг друга, так что сильный «угловой» сигнал уничтожит более слабые «кривые» сигналы.Таким образом, даже если изображение знака остановки может вызвать небольшую «кривую» реакцию в некоторых клетках мозга, «угловой» сигнал отключает ее, и вы видите угловатую форму.
Но когда вы пристально смотрите на фигуру, эти клетки истощаются, так же как клетки сетчатки адаптируются к одному цвету. Вот здесь и проявляется иллюзия.
«Когда один детектор устает из-за длительного наблюдения, другой детектор доминирует», — сказал Ито. «Таким образом, круг и шестиугольник меняют форму в остаточных изображениях.«
Ито планирует работать с нейробиологами, чтобы измерить активность мозга и определить эти клетки, определяющие кривые и углы. Он также следит за другими примерами странных визуальных иллюзий, — сказал он.
« Люди склонны думать, что это остаточные изображения. — бессмысленные побочные продукты, возникающие из-за физиологических характеристик глаза, — написал Ито в электронном письме APS. — Но я думаю, что остаточные изображения отражают деятельность мозга и дают нам возможность узнать об этой активности в непосредственно видимой форме.»
Вы можете следить за LiveScience старшим писателем Стефани Паппас в Twitter @sipappas . Следите за LiveScience, чтобы следить за последними научными новостями и открытиями в Twitter @livescience и на Facebook .
Круги в прямоугольнике
Калькулятор ниже оценивает максимальное количество кругов, которые могут поместиться в прямоугольнике. Калькулятор можно использовать для расчета
- количества труб или проводов, которые подходят для кабелепровода или аналогичных приложений.
Введите внутренние размеры прямоугольника — высоту и ширину и внешние диаметры окружностей.
Значения по умолчанию для кругов 0,5 дюйма внутри квадрата 10 дюймов x 10 дюймов . Калькулятор является универсальным, и можно использовать любые единицы измерения, если одни и те же единицы используются для всех значений.
Прямоугольный узор

Прямоугольный узор — координаты окружности
Скопируйте и вставьте координаты центра окружности в ваше приложение. x = 0 и y = 0 — это верхний левый угол прямоугольника.
x y
Совет! — значения могут быть адаптированы и изменены в Excel или текстовом редакторе для использования в генераторе G-кода ЧПУ или аналогичном.
Треугольный узор

Треугольный узор — координаты круга
Скопируйте и вставьте координаты центра круга в свое приложение. x = 0 и y = 0 — это верхний левый угол прямоугольника.
x y
Внимание! — Алгоритм довольно прост — переключение ширины и высоты прямоугольника может повлиять на вычисляемое число.Переключение введенных выше значений изменяет макет и дает
Примечание! — с некоторыми комбинациями прямоугольных форм и размеров кругов — еще один или два круга — или даже больше — могут быть добавлены с измененным расположением кругов. В приведенном выше примере треугольника по умолчанию — еще два круга могут быть добавлены между ними, если левый и правый нижние круги перемещены к левой и правой границе. Алгоритм, используемый для расчета, довольно прост и в некоторых случаях может недооценивать количество кругов.
.