Как построить десятиугольник: Как начертить десятиугольник 🚩 как построить правильный десятиугольник 🚩 Математика

геометрические построения | Справочник по математике

На отрезке ВК, равном 2а, как и на диаметре, строим (рис.1) полукруг. Этот полукруг делим на n равных частей точками C, D, E, F, G (вершинами правильного вписанного 2n-угольника; на нашем рисунке n=6). Центр А соединяем лучами со всеми полученными точками, кроме двух последних (K и G). Из точки В радиусом АВ проводим дугу ab, засекая на луче AD точку М и т.д. Точки B, L, M, N и т.д. последовательно соединяем прямыми. Многоугольник ABLMNF – искомый.

рис.1

Решить эту задачу с помощью циркуля и линейки можно не всегда; например, при n=7, n=9 этого сделать нельзя, так как полукруг с помощью циркуля и линейки на 7 или 9 точно не делится.

Запись опубликована 12. 10.2014 автором admin в рубрике Геометрия с метками геометрические построения, многоугольник.

Отметим на окружности (рис.1) вершины A, B, …, F правильного вписанного многоугольника с тем же числом сторон (см. §33 и §36). Проведем радиусы ОА, ОВ, …, OF и продолжим их. Дугу АВ разделим пополам точкой Е (см. §15). Через Е проведем JP⊥OE. Отрезок JP, заключенный между продолжениями соседних радиусов, есть сторона искомой фигуры. На продолжении остальных радиусов откладываем отрезки ОК, OL, …, ON, равные OP

. Точки J, K, L, …, N, P последовательно соединяем. Многоугольник JKLM…NP – искомый.

рис.1

Запись опубликована 12.10.2014 автором admin в рубрике Геометрия с метками геометрические построения, многоугольник, окружность.

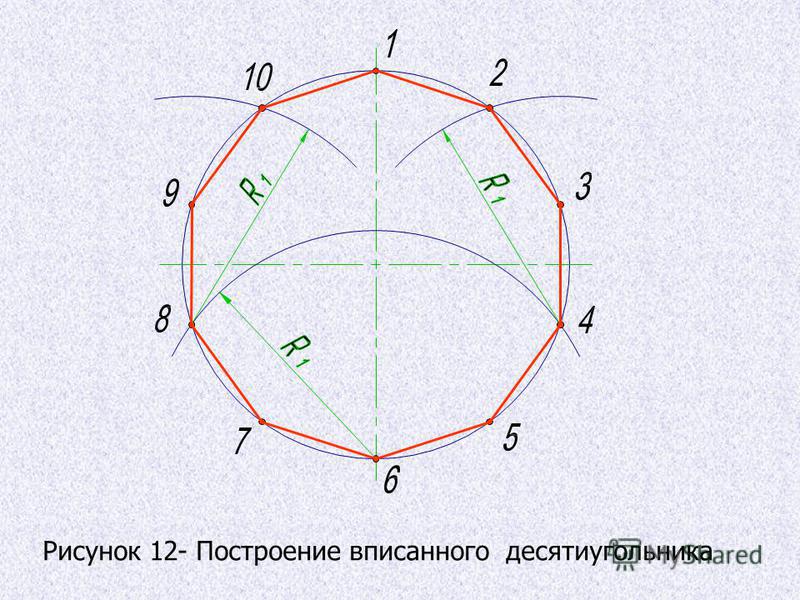
Построим точку F (рис.1), как и в §33 OF есть сторона искомой фигуры. Раствором циркуля, равным OF, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры

рис.1

Запись опубликована 12.10.2014 автором admin в рубрике Геометрия с метками геометрические построения, десятиугольник, круг, многоугольник, окружность.

Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Разделив пополам дуги AD, DB, BC, CA точками E, F, G, H (см. §15), последовательно соединяем полученные восемь точек.

рис.1

Запись опубликована 12.10.2014 автором admin в рубрике Геометрия с метками восьмиугольник, геометрические построения, круг, многоугольник, окружность.

Раствором циркуля, равным радиусу круга, делаем на окружности засечки в точках

A, B, C, D, E, F (рис. 1). Соединяя точки A, B, C, D, E, F подряд, получим правильный шестиугольник. Соединяя их через одну, получим правильный (равносторонний) треугольник.

рис.1

Запись опубликована 12.10.2014 автором admin в рубрике Геометрия с метками геометрические построения, многоугольник, треугольник, шестиугольник.

Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Делим пополам радиус АО точкой Е. Из Е радиусом ЕС проводим дугу CF, пересекая ее диаметр АВ в точке F. Из С радиусом CF проводим дугу FG, пересекая ею данную окружность в точке G; CG(=CF) есть одна сторона искомой фигуры. Проводим тем же радиусом дугу mn из точки П как из центра, получаем еще одну вершину H искомой фигуры и т.д.

рис.1

Запись опубликована 12.10.2014 автором admin в рубрике Геометрия с метками геометрические построения, круг, многоугольник, окружность, пятиугольник.

Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Из их концов, как из центров, описываем четыре полуокружности радиусами, равными ОА. Точки F, G, H и E их пересечения – вершины искомого квадрата.

рис.1

Запись опубликована 10.10.2014 автором admin в рубрике Геометрия с метками геометрические построения, квадрат, круг, многоугольник, окружность.

Проводим два взаимно перпендикулярных диаметра АВ и СD; ACBD – искомый квадрат (рис.1)

рис.1

Запись опубликована

10.10.2014 автором admin в рубрике Геометрия с метками геометрические построения, квадрат, круг, многоугольник, окружность.

Через середину АВ (рис.1) проводим к АВ перпендикуляр MN (см. п. §2). От точки О его пересечения с АВ откладываем на MN отрезки ОС и OD, равные ОА; соединяем точки С и D с точками А и В; ABCD – искомый квадрат.

рис.1

Запись опубликована 09.10.2014 автором admin в рубрике Геометрия с метками геометрические построения, квадрат, многоугольник.

Поступаем как в пп. §27 и §28

Запись опубликована 09.10.2014 автором admin в рубрике Геометрия с метками геометрические построения, квадрат, многоугольник.

Свежие записи

• Умножение двузначных чисел, оканчивающихся на 1
• Фигурные числа
• Многочлен
• Признаки делимости на 2,3,4,5,6,7,8,9,10,11,25,100,1000
• Математические софизмы. Логические парадоксы

Архивы

• Ноябрь 2020
• Апрель 2020
• Май 2018
• Сентябрь 2017
• Октябрь 2015
• Сентябрь 2015
• Июль 2015
• Апрель 2015
• Март 2015
• Октябрь 2014
• Сентябрь 2014

Рубрики

• GIFки
• Алгебра
• Арифметика
• Геометрия
• Загадки
• Как посчитать
• Новости
• Тригонометрия
• Функции и графики
• Энциклопедия

Внешние биллиарды вне правильного десятиугольника: периодичность почти всех орбит и существование апериодической орбиты | Рухович

Филипп Дмитриевич Рухович

https://doi.org/10.22405/2226-8383-2019-20-2-406-441

PDF (Rus)

• Аннотация
• Об авторе
• Список литературы

Аннотация

Внешние биллиарды были введены Б.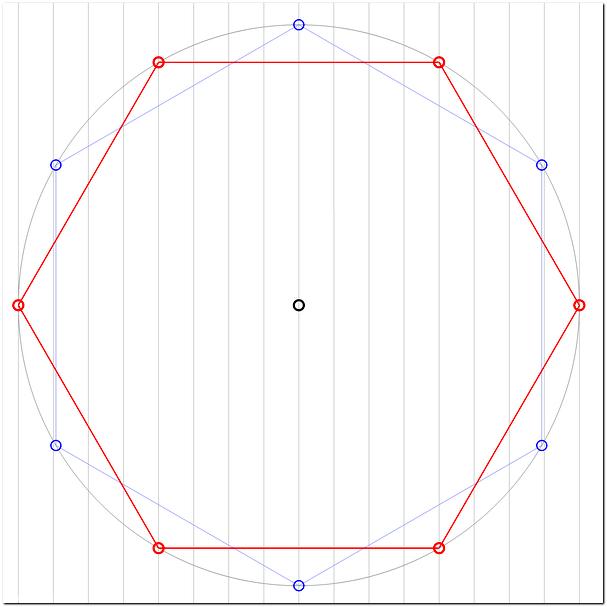 Нойманном в 50-х годах ХХ века и стали популярны в 70-х благодаря Ю. Мозеру, который рассматривал внешний, или двойственный, биллиард как игрушечную модель небесной механики. Задача об устойчивости Солнечной системы обладает тем свойством, что «легко выписать n уравнений движения частиц, но сложно понять это движение интуитивно»; в связи с этим, Мозер предложил рассмотреть ранее поставленную Б. Нойманном задачу внешнего биллиарда, обладающую тем же свойством.

Одним из классических примеров динамической систем является внешний биллиард вне правильного ????-угольника; в частности, с ним связаны проблемы существования апериодической траектории, а также полноты периодических точек. Эти проблемы решены лишь для ограниченного количества частных случаев.
При ???? = 3, 4, 6 стол является решеточным, и, как следствие, апериодических точек нет, а периодические точки образуют множество полной меры. В 1993 году, С. Табачникову удалось найти апериодическую точку в случае правильного пятиугольника; сделано это было с помощью ренормализационной схемы — метода, имеющего фундаментальное значение при исследовании самоподобных динамических систем.

По мнению Р. Шварца, следующими по сложности являются случаи n = 10,8,12; в этих случаях, а также в случае ???? = 5 для внешнего биллиарда удается построить ренормализационную схему, которая, как пишет Шварц, “позволяет дать (как минимум, в принципе) полное описание того, что происходит”.
Позже, автору удалось обнаружить самоподобные структуры и построить ренормализационную схему для случаев правильных восьми- и двенадцатиугольника.
Данная же статья посвящена внешнему биллиарду вне правильного десятиугольника. Доказано существование апериодической орбиты для внешнего биллиарда вне правильного десятиугольника, а также, что почти все траектории такого внешнего биллиарда являются периодическими; явно выписаны все возможные периоды. В основе работы лежит классическая технология поиска и исследования ренормализационной схемы. Возникающие в случае ???? = 10 периодические структуры похожи на периодические структуры в случае ???? = 5, но все же имеют свои особенности.

Об авторе

Филипп Дмитриевич Рухович

Россия

Список литературы

1. Rukhovich F. Outer billiards outside a regular octagon: periodicity of almost all orbits and existence of an aperiodic orbit. // Doklady Mathematics, 2018, Vol. 98, Issue 1, pp. 334–337.

2. Rukhovich F. Outer billiards outside regular dodecagon: computer proof of periodicity of almost all orbits and existence of an aperiodic point. // arXiv:1809.03791, 2018

3. Табачников С. Внешние биллиарды // Успехи математических наук, 1993. T. 48. Вып. 6(294). С. 75–102.

4. Moser J. Is the solar system stable? // Math. Intell., 1978, Vol. 1. P. 65–71.

5. Schwartz, R. E. Outer billiards on kites // Annals of Mathematics Studies — Princeton University Press, Princeton, NJ, 2009. Vol. 171.

6. Dolgopyat, D., Fayad, B. Unbounded orbits for semicircular outer billiard // Ann. Henri Poincare, 2009. Vol. 10, issue 2. P. 357–375.

7. Bedaride, N., Cassaigne, J. Outer billiards outside regular regular polygons // Journal of the London Mathematical Society, 2011.

8. Tabachnikov, S. Geometry and Billiards // Student Mathematical Library — American Mathematical Society, Providence, RI, 2005. Vol. 30.

9. Tabachnikov, S. On the dual billiard problem // Adv. Math, 1995. Vol. 115, № 2. P. 221–249.

10. Bedaride, N., Cassaigne, J. Outer billiards outside regular regular polygons // eprint arXiv:0912.0563, 2011.

11. Schwartz, R. E. Outer Billiards, Arithmetic Graph and the Octagon // eprint arXiv:1006.2782, 2010.

12. Schwartz, R. E. The octagonal PETs // Mathematical Surveys and Monographs — American Mathematical Society, Providence, RI, 2014. Vol. 197.

13. N. Pytheas Fogg. Substitutions in dynamics, arithmetics and combinatorics // Lecture Notes in Mathematics. Edited by V. Berth’e, S. Ferenczi, C. Mauduit and A. Siegel. — Springer-Verlag, Berlin, 2002. Vol. 1794.

14. Shaidenko. A, Vivaldi F. Global stability of a class of discontinuous dual billiards // Comm. Math. Phys., 1987. Vol. 110. P. 625—640.

15. Kolodziej, R. The antibilliard outside a polygon // Bull. Pol. Acad. Sci., 1989. Vol. 37. P. 163–168.

16. Gutkin, E., Simanyi, N. Dual polygonal billiards and necklace dynamics // Comm. Math. Phys., 1991. Vol. 143. P. 431—450.

17. Jeong, I.J. Outer billiards with contraction: regular polygons. // Dynamical Systems, 2015. Vol. 33, № 4. P. 565–580; DOI: 10.1080/14689367.2017.1402295

Рецензия

Для цитирования:

---

Рухович Ф.Д. Внешние биллиарды вне правильного десятиугольника: периодичность почти всех орбит и существование апериодической орбиты. Чебышевский сборник. 2019;20(2):406-441. https://doi.org/10.22405/2226-8383-2019-20-2-406-441

For citation:

---

Rukhovich F.D. Outer billiards outside regular decagon: periodicity of almost all orbits and existence of aperiodic orbit. Chebyshevskii Sbornik. 2019;20(2):406-441. (In Russ.) https://doi.org/10.22405/2226-8383-2019-20-2-406-441

Просмотров: 412

Контент доступен под лицензией Creative Commons Attribution 4.0 License.

Десятиугольник – форма, определение, формула, примеры

В геометрии десятиугольник известен как десятисторонний многоугольник или десятиугольник. Сумма внутренних углов простого десятиугольника равна 1440°, а сумма внешних углов десятиугольника равна 360°.

1.	Значение Декагона
2.	Типы Decagon
3.	Свойства Decagon
4.	Формулы Декагона
5.	Часто задаваемые вопросы о Decagon

Значение Декагона

Десятиугольник — это десятигранный многоугольник с десятью вершинами и десятью углами. Таким образом, форму десятиугольника можно определить как многоугольник с десятью сторонами, десятью внутренними углами и десятью вершинами. Основываясь на сторонах десятиугольника, они в целом подразделяются на правильные десятиугольники и неправильные десятиугольники. В правильном десятиугольнике 35 диагоналей и 8 треугольников. Расположение этих диагоналей и треугольников объясняется в следующих разделах этой статьи.

Типы Decagon

Десятиугольники можно разделить на правильные и неправильные десятиугольники на основе размеров сторон и углов. Существует три возможных классификации десятиугольников, которые приведены ниже:

• Правильные и неправильные десятиугольники
• Выпуклые и вогнутые десятиугольники
• Простые и сложные десятиугольники

Правильный десятиугольник

Правильный десятиугольник — это многоугольник с 20 равными сторонами и 10 вершинами. Стороны и углы равны в правильном десятиугольнике.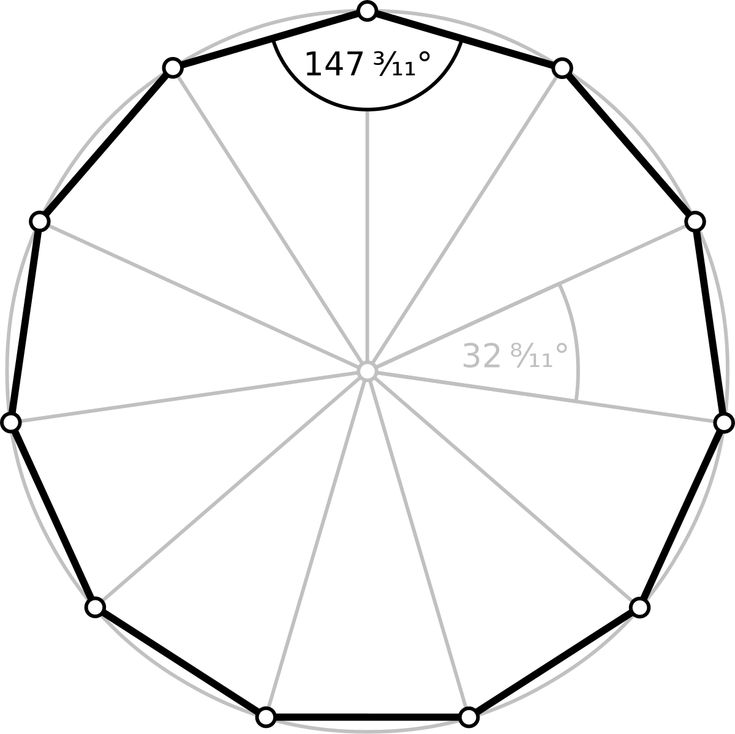 Характеристики правильного десятиугольника:

• Все стороны равны по длине и все углы равны по размеру в правильном десятиугольнике.
• Каждый внутренний угол правильного десятиугольника равен 144º, а каждый внешний угол равен 36º.

Неправильный десятиугольник

Неправильный десятиугольник не имеет равных сторон и углов. По крайней мере, две стороны и углы различны в измерении. Посмотрите на приведенные ниже изображения, на которых показаны неправильные десятиугольники.

Выпуклые и вогнутые десятиугольники

Как и любой другой многоугольник, десятиугольник также может быть выпуклым и вогнутым. Выпуклый десятиугольник выпирает наружу, так как все внутренние углы меньше 180°. В то время как вогнутые декагоны имеют углубления (глубокую выемку). По крайней мере, один из внутренних углов больше 180 ° в вогнутых десятиугольниках.

Простые и сложные десятиугольники

Простые десятиугольники относятся к десятиугольникам, стороны которых не пересекаются. Они следуют всем вышеперечисленным правилам обычного десятиугольника. В то время как сложные десятиугольники относятся к самопересекающимся десятиугольникам и имеют дополнительные внутренние пространства. Они не следуют строго каким-либо предписанным правилам десятиугольников относительно их внутренних углов и их сумм.

Свойства Decagon

Здесь перечислены некоторые важные свойства десятиугольников.

• Сумма внутренних углов равна 1440°.
• Сумма измерений внешнего угла составляет 360°.
• Центральный угол правильного десятиугольника составляет 36 градусов.
• В десятиугольнике 35 диагоналей.
• В десятиугольнике 8 треугольников.

Сумма внутренних углов десятиугольника

Чтобы найти сумму внутренних углов десятиугольника, сначала разделите его на треугольники. В правильном десятиугольнике восемь треугольников. Мы знаем, что сумма углов каждого треугольника равна 180°. Таким образом, 180° × 8 = 1440°. Следовательно, сумма всех внутренних углов десятиугольника равна 1440°.

Мы знаем, что количество сторон десятиугольника равно 10. Следовательно, делим общую сумму внутренних углов на 10

1440° ÷ 10 = 144°

Таким образом, один внутренний угол правильного десятиугольника равен 144°. А сумма всех внутренних углов десятиугольника равна 1440°.

Мера центральных углов правильного десятиугольника

Чтобы найти меру центрального угла правильного десятиугольника, нам нужно начертить окружность посередине. Окружность образует 360°. Разделите это число на десять, потому что у десятиугольника 10 сторон. 360° ÷ 10 = 36°. Таким образом, центральный угол правильного десятиугольника равен 36°.

Десятиугольные диагонали

Диагональ — это линия, которую можно провести из одной вершины в другую. Количество диагоналей многоугольника рассчитывается как: n(n−3) ÷ 2. В десятиугольнике n — это количество сторон, равное 10, поэтому n=10. Теперь мы получаем,
n(n−3) ÷ 2 = 10(10−3) ÷ 2
Таким образом, количество диагоналей в десятиугольнике равно 35.

В десятиугольнике 8 треугольников

При соединении одной вершины с остальными вершинами десятиугольника получится 8 треугольников. Соединив все вершины независимо друг от друга, получится 80 треугольников (8×10). Посмотрите на изображение, приведенное ниже, на котором показаны диагонали и треугольники десятиугольника. 92}{2} \times \sqrt{5 + 2\sqrt{5}}\), где a – длина стороны десятиугольника.

Формула для нахождения периметра правильного десятиугольника: 10 раз больше стороны или 10 × n, где n — длина стороны десятиугольника (поскольку все стороны равны, а общее количество сторон равно 10). В случае неправильного десятиугольника мы можем просто сложить длины сторон, чтобы найти периметр.

Важные примечания

• У десятиугольника десять сторон.
• Сумма внутренних углов десятиугольника равна 1440°.
• Сумма внешних углов десятиугольника равна 360°.
• В правильном десятиугольнике 35 диагоналей.
• Десятиугольники можно разделить на правильные, неправильные, выпуклые, вогнутые, простые и сложные.

Статьи по теме

Ознакомьтесь с этими интересными статьями, чтобы узнать больше о десятиугольнике и связанных с ним темах.

• Площадь десятиугольника
• Додекагон
• Сколько осей симметрии имеет правильный десятиугольник?

Часто задаваемые вопросы о Decagon

Что такое десятиугольник в геометрии?

Десятиугольник можно распознать как многоугольник с 10 сторонами, 10 внутренними углами и 10 вершинами. Декагон может быть правильным и неправильным. У правильного десятиугольника все стороны равны. Неправильный десятиугольник имеет неравные стороны.

Как найти площадь десятиугольника?

Формула для нахождения площади правильного десятиугольника: 5a ² /2 × \(\sqrt{5 + 2\sqrt{5}}\), где a — размер стороны десятиугольника. Если нам известна длина стороны правильного десятиугольника, то мы можем использовать эту формулу, чтобы найти площадь. Не существует формулы для нахождения площади неправильного десятиугольника, но мы можем разделить его на треугольники и попытаться найти площади всех треугольников и сложить их.

Сколько сторон у десятиугольника?

Согласно свойствам десятиугольника, общее количество сторон равно 10, полученных путем соединения 10 вершин. Поскольку имеется только 10 сторон и 10 вершин, количество внутренних и внешних углов, образованных всеми 10 сторонами, также равно 10.

Сколько вершин и диагоналей имеет правильный десятиугольник?

Правильный десятиугольник имеет 10 вершин и 35 диагоналей. Диагонали десятиугольника находятся по формуле n(n-3) ÷ 2, где n — количество сторон, равное 10. Таким образом, 10(10-3) ÷ 2 = 35,

Каковы внешние углы правильного десятиугольника?

Внешние углы десятиугольника — это внешние углы, образованные двумя сторонами, соединенными одной вершиной десятиугольника. Каждый внешний угол примыкает к соответствующему внутреннему углу и образует 180 градусов в вершине десятиугольника. В правильном десятиугольнике все углы равны. Сумма всех внешних углов правильного десятиугольника равна 360°. Так как в десятиугольнике 10 сторон.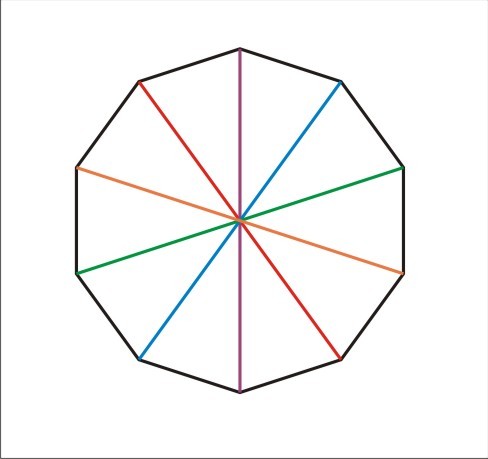 Следовательно, каждый внешний угол равен 36° (360° ÷ 10 = 36°).

Какова сумма внутренних углов десятиугольника?

Сумма всех внутренних углов десятиугольника равна 1440°. Существует формула для нахождения суммы внутренних углов n-стороннего многоугольника [(n-2)(180)], где n равно количеству сторон. Таким образом, сумма внутренних углов десятиугольника = (10-2) × 180° = 1440°. Кроме того, меру каждого внутреннего угла в правильном десятиугольнике можно найти, разделив сумму на общее количество сторон в десятиугольнике ⇒ 1440/10 = 144°.

Как называется 10-сторонняя фигура?

Десятиугольник известен как десятигранная фигура или многоугольник с десятью вершинами и десятью углами. Когда любая фигура образуется путем соединения 10 сторон, она называется десятиугольником.

Геометрические свойства десятиугольника | calcresource

Перейти к

—  Калькулятор

—  Теоретические основы

РЕКЛАМА

Калькулятор обычного десятиугольника

— Д-р Минас Э. Лемонис, доктор философии — Обновлено: Home 00 9 9 декабря 2020 г.0003

Этот инструмент вычисляет основные геометрические свойства правильного десятиугольника. Правильные многоугольники равносторонние (все стороны равны), а также все углы равны. Инструмент может рассчитать свойства десятиугольника, учитывая либо длину его сторон, либо внутренний радиус, либо радиус описанной окружности, либо площадь, либо высоту, либо ширину. Введите ниже размеры формы. Вычисленные результаты будут иметь те же единицы измерения, что и введенные вами. Пожалуйста, используйте согласованные единицы для любых входных данных.

0051 rad

Known data:

Side length Inradius Circumradius Area Height Width

Geometric properties:

Area =

Периметр =

α = 920006 80266

R i =

R c =

ADVERTISEMENT

Bounding box:

Height H =

Ширина W =

Углы:

DEG

DEG

DEG

Interior φ =

Central θ =

Share this

Table of Contents

— Калькулятор

— Теоретические основы

— Определения

— Свойства правильных десятиугольников

— Симметрия

— Внутренний угол и центральный угол

-круговой округ и инвентарь

-Площадь и периметр

-Ограничивающая коробка

-Как нарисовать обычный декагон

-Примеры

-Регулярный чит -лист Decagon

-См. Также

РЕКЛАМА.0003

-круговой округ и инвентарь

-Площадь и периметр

-Ограничивающая коробка

-Как нарисовать обычный декагон

-Примеры

-обычный декаговый чит

-см. Также

Определения

Decagon. многоугольник с десятью сторонами и десятью вершинами. Десятиугольник, как и любой другой многоугольник, может быть выпуклым или вогнутым, как показано на следующем рисунке. У выпуклого десятиугольника ни один из внутренних углов не превышает 180°. Напротив, вогнутый десятиугольник (или многоугольник) имеет один или несколько внутренних углов больше 180 °. Десятиугольник называется правильным, если его стороны равны, а внутренние углы равны . В этом отношении недостаточно иметь только равные стороны, поскольку десятиугольник может быть вогнутым с равными сторонами. Как показано на рисунке ниже, можно определить множество возможных вогнутых десятиугольников с равными сторонами, но неравными внутренними углами. Эти десятиугольники называются равносторонними. Любой десятиугольник, который не является правильным, называется неправильным.

Сумма внутренних углов любого десятиугольника, выпуклого или вогнутого, всегда равна 1440°. Это легко доказать, посчитав, сколько треугольников можно поместить внутрь десятиугольника. Чтобы выяснить это, мы должны провести прямые линии между всеми вершинами, избегая пересечений. В результате получается ровно восемь треугольников. Даже через вершины можно соединять по-разному (в результате получаются разные треугольники), число треугольников всегда остается восемью. Сумма внутренних углов в одном треугольнике равна 180°, поэтому для 8 треугольников, стоящих рядом, сумма углов должна составлять 8×180=1440°.

Диагонали десятиугольника делят его внутреннюю часть на 8 треугольников

Свойства правильных десятиугольников

Симметрия

В правильном десятиугольнике десять осей симметрии. Пять из них проходят через диагонально противоположные вершины, а остальные пять проходят через середины противоположных ребер. Все оси встречаются в одной точке, центре десятиугольника.

Оси симметрии правильного десятиугольника

РЕКЛАМА

Внутренний угол и центральный угол

9\circ

Во внутреннем треугольнике, образованном двумя последовательными диагоналями и ребром десятиугольника, два угла, прилежащие к ребру, равны 72°. Это действительно \varphi/2, потому что диагонали десятиугольника также являются осями симметрии, таким образом делящие пополам внутренние углы \varphi (которые равны 144°).

Внутренний и центральный углы дополнительные, так как их сумма равна 180°:

\varphi+\theta=144°+36°=180°

Это свойство является общим для всех правильных многоугольников.

Окружность и вписанная окружность

Можно нарисовать окружность, проходящую через все десять вершин правильного десятиугольника. Это описанная окружность или описанная окружность . Центр этого круга также является центром десятиугольника. Диагонали правильного десятиугольника, соединяющие противоположные вершины, являются диаметрами описанной окружности. Радиус описанной окружности R_c обычно называют радиусом описанной окружности .

Можно также нарисовать еще одну окружность, проходящую через середины всех десяти ребер десятиугольника. Этот круг называется вписанным кругом или обведите . Радиус вписанной окружности R_i обычно называют inradius . Вписанная окружность касается всех десяти ребер и имеет один и тот же центр с описанной окружностью.

Все правильные многоугольники имеют описанную и вписанную окружности.

Описанные и вписанные окружности правильного десятиугольника

Радиусы описанной и вписанной окружности, R_c и R_i, соответственно, связаны с длиной ребра, \alpha. Соответствующие отношения можно найти, используя прямоугольный треугольник, выделенный на следующем рисунке, со следующими сторонами: радиус описанной окружности, внутренний радиус и половина ребра десятиугольника. Используя базовую тригонометрию, мы можем найти:

\begin{split} R_c & = \frac{a}{2 \sin{\frac{\theta}{2}}} \\ R_i & = \frac{a}{2 \tan{\frac{\ theta}{2}}} \\ R_i & = R_c \cos{\frac{\theta}{2}} \end{split}

, где \theta — центральный угол, а \alpha — длина ребра. {\circ}} \end{split}.

Кроме того, приближения для радиуса описанной окружности и внутреннего радиуса десятиугольника задаются следующими формулами: Общая площадь правильного десятиугольника может быть разделена на 10 одинаковых равнобедренных треугольников, как показано на рисунке ниже. Высота любого из этих треугольников, перпендикулярная ребру десятиугольника a, действительно является радиусом вписанной окружности, поэтому его длина равна R_i. Следовательно, площадь каждого треугольника должна быть равна \frac{1}{2}a R_i, и в результате общая площадь восьми треугольников составит: 92

Периметр любого N-стороннего правильного многоугольника представляет собой просто сумму длин всех ребер: P = N a . Таким образом, для правильного десятиугольника с 10 ребрами:

P = 10a

Ограничивающая рамка

Ограничивающая рамка плоской фигуры — это наименьший прямоугольник, полностью охватывающий фигуру. Размеры этого прямоугольника определяются высотой h и шириной w. Интуитивно можно определить ограничивающий прямоугольник обычного прямоугольника, как показано на следующем рисунке: 9\circ}}

аппроксимируется следующим образом:

w=3.236a

Как нарисовать правильный десятиугольник

Правильный десятиугольник можно построить, используя только линейку и циркуль, учитывая его радиус описанной окружности. Процедура описана следующими шагами и проиллюстрирована на рисунке ниже:

1. Сначала просто нарисуйте линию (чуть больше желаемого диаметра описанной окружности).
2. Отметьте на линии две точки: одна — центр многоугольника (точка O), а другая — точка описанной окружности (точка A). Расстояние OA является радиусом описанной окружности R_c. Нарисуйте окружность вокруг центральной точки, которая проходит через точку A. Это описанная окружность. Отметьте еще одну точку, где описанная окружность пересекается с линией (точка B).
3. Затем постройте дугу окружности с центром в точке A и радиусом немного большим, чем R_c.
4. Также дуга окружности с центром в точке B и тем же радиусом, что и в шаге 3. Отметьте две точки, в которых две дуги пересекаются.
5. Нарисуйте линию, проходящую через точки пересечения двух дуг из последнего шага (также проходящую через центральную точку О) и отметьте еще две точки, 1 и 6, где эта линия пересекается с описанной окружностью.
6. Поместите конец циркуля в точку A и постройте новую дугу окружности, проходящую через центральную точку O. Отметьте две точки, в которых дуга пересекается с описанной окружностью.
7. Нарисуйте линию, проходящую через две точки пересечения из предыдущего шага. Отметьте точку М, где эта линия пересекается с линейным отрезком ОА.
8. Проведите линию от точки 1 до точки M.
9. Поместите кончик циркуля в точку M и нарисуйте дугу окружности, проходящую через центральную точку O. Отметьте точку N, где эта дуга пересекается с линией, проведенной в предыдущий шаг.
10. Поместив кончик циркуля в точку 1, начертите дугу окружности, проходящую через точку N. Отметьте две точки 2 и 10, где дуга пересекается с описанной окружностью.
11. Используя тот же радиус, нарисуйте дугу окружности с центром вокруг точки 2 и отметьте точку 3, где дуга пересекается с описанной окружностью.
12. Повторите последний шаг, на этот раз, используя точку 3 в качестве центра дуги. В результате точка 4 определяется на пересечении с описанной окружностью. Продолжайте в том же духе, рисуя дуги и отмечая точки вокруг описанной окружности.
13. На данный момент вокруг описанной окружности должно быть отмечено десять точек, от 1 до 10. Это вершины десятиугольника. Нарисуйте линейные сегменты между ними, и теперь правильный десятиугольник готов.

На следующем рисунке показана пошаговая процедура рисования.

На рисунке показано, как нарисовать правильный десятиугольник с помощью линейки и циркуля.

РЕКЛАМА

Примеры

Пример 1

Определите радиус описанной окружности, внутренний радиус и площадь правильного десятиугольника с длиной ребра a=7».

No related posts.